спецификации, руководства, описания, API

Содержание | Предыдущий | Следующий | Индекс

20.11 Класс `java.lang.Math`

Класс Math содержит полезные основные числовые константы и методы.

public final class Math {
	public static final double E = 2.7182818284590452354;
	public static final double PI = 3.14159265358979323846;
	public static double sin(double a);
	public static double cos(double a);
	public static double tan(double a);
	public static double asin(double a);
	public static double acos(double a);
	public static double atan(double a);
	public static double atan2(double a, double b);
	public static double exp(double a);
	public static double log(double a);
	public static double sqrt(double a);
	public static double pow(double a, double b);
	public static double IEEEremainder(double f1, double f2);
	public static double ceil(double a);
	public static double floor(double a);
	public static double rint(double a);
	public static int round(float a);
	public static long round(double a);
	public static double random();
	public static int abs(int a);
	public static long abs(long a);
	public static float abs(float a);
	public static double abs(double a);
	public static int min(int a, int b);
	public static long min(long a, long b);
	public static float min(float a, float b);
	public static double min(double a, double b);
	public static int max(int a, int b);
	public static long max(long a, long b);
	public static float max(float a, float b);
	public static double max(double a, double b);
}

Чтобы гарантировать мобильность программ Java, спецификации многих из числовых функций в этом пакете требуют, чтобы они привели к тем же самым результатам как определенные опубликованные алгоритмы. Эти алгоритмы доступны от известной сетевой библиотеки netlib как пакет fdlibm ("Свободно Распространяемая Математическая Библиотека"). Эти алгоритмы, которые пишутся в языке программирования C, должны быть поняты как будто выполняемый в порядке выполнения Java со всеми операциями с плавающей точкой после правил Java арифметика с плавающей точкой.

Сетевая библиотека может быть найдена в http://netlib.att.com во всемирной паутине; тогда выполните поиск по ключевым словам fdlibm. Библиотека может также быть получена Электронной почтой; чтобы начать процесс, отправьте сообщение, содержащее строку:

send index from fdlibm

к netlib@research.att.com. Математическая библиотека Java определяется относительно версии fdlibm датированный 04.01.95. Где fdlibm обеспечивает больше чем одно определение для функции (такой как acos), "версия" функции ядра IEEE754 должна использоваться (нахождение в файле, имя которого начинается с буквы e).

Полное и автономное описание алгоритмов, которые будут использоваться для этих функций, будет обеспечено в будущей версии этой спецификации. Также ожидается, что алгоритмы будут кодированы в Java, чтобы обеспечить ссылочную реализацию, которая не связывается к fdlibm.

20.11.1 public static final double E = 2.7182818284590452354;

Постоянная величина этого поля double значение, которое ближе чем любой другой к e, основе натуральных логарифмов.

20.11.2 public static final double PI = 3.14159265358979323846;

Постоянная величина этого поля double значение, которое ближе чем любой другой к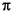, отношение окружности круга к его диаметру.

20.11.3 public static double sin(double a)

Этот метод вычисляет приближение к синусу параметра, используя sin алгоритм как публикующийся в fdlibm (см. введение в этот раздел).

Особые случаи:

Если параметром является НЭН или бесконечность, то результатом является НЭН.
Если параметром является положительный нуль, то результатом является положительный нуль; если параметром является отрицательный нуль, то результатом является отрицательный нуль.

20.11.4 public static double cos(double a)

Этот метод вычисляет приближение к косинусу параметра, используя cos алгоритм как публикующийся в fdlibm (см. введение в этот раздел).

Особый случай:

Если параметром является НЭН или бесконечность, то результатом является НЭН.

20.11.5 public static double tan(double a)

Этот метод вычисляет приближение к касательной параметра, используя tan алгоритм как публикующийся в fdlibm (см. введение в этот раздел).

Особые случаи:

Если параметром является НЭН или бесконечность, то результатом является НЭН.
Если параметром является положительный нуль, то результатом является положительный нуль; если параметром является отрицательный нуль, то результатом является отрицательный нуль.

20.11.6 public static double asin(double a)

Этот метод вычисляет приближение к арксинусу параметра, используя asin алгоритм как публикующийся в fdlibm (см. введение в этот раздел).

Особые случаи:

Если параметром является НЭН, или его абсолютное значение больше чем 1, то результатом является НЭН.
Если параметром является положительный нуль, то результатом является положительный нуль; если параметром является отрицательный нуль, то результатом является отрицательный нуль.

20.11.7 public static double acos(double a)

Этот метод вычисляет приближение к арккосинусу параметра, используя acos алгоритм как публикующийся в fdlibm (см. введение в этот раздел).

Особый случай:

Если параметром является НЭН, или его абсолютное значение больше чем 1, то результатом является НЭН.

20.11.8 public static double atan(double a)

Этот метод вычисляет приближение к арктангенсу параметра, используя atan алгоритм как публикующийся в fdlibm (см. введение в этот раздел).

Особые случаи:

Если параметром является НЭН, то результатом является НЭН.
Если параметром является положительный нуль, то результатом является положительный нуль; если параметром является отрицательный нуль, то результатом является отрицательный нуль.

20.11.9 public static double atan2(double y, double x)

Этот метод вычисляет приближение к арктангенсу частного 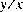параметров, используя atan2 алгоритм как публикующийся в fdlibm (см. введение в этот раздел).

Особые случаи:

Если любым параметром является НЭН, то результатом является НЭН.
Если первым параметром является положительный нуль, и второй параметр положителен, или первый параметр положителен и конечен, и вторым параметром является положительная бесконечность, то результатом является положительный нуль.
Если первым параметром является отрицательный нуль, и второй параметр положителен, или первый параметр отрицателен и конечен, и вторым параметром является положительная бесконечность, то результатом является отрицательный нуль.
Если первым параметром является положительный нуль, и второй параметр отрицателен, или первый параметр положителен и конечен, и вторым параметром является отрицательная бесконечность, то результат double оцените самый близкий к.
Если первым параметром является отрицательный нуль, и второй параметр отрицателен, или первый параметр отрицателен и конечен, и вторым параметром является отрицательная бесконечность, то результат double оцените самый близкий к.
Если первый параметр положителен, и вторым параметром является положительный нулевой или отрицательный нуль, или первым параметром является положительная бесконечность, и второй параметр конечен, то результат double оцените самый близкий к.
Если первый параметр отрицателен, и вторым параметром является положительный нулевой или отрицательный нуль, или первым параметром является отрицательная бесконечность, и второй параметр конечен, то результат double оцените самый близкий к.
Если обоими параметрами является положительная бесконечность, то результат double оцените самый близкий к.
Если первым параметром является положительная бесконечность, и вторым параметром является отрицательная бесконечность, то результат double оцените самый близкий к.
Если первым параметром является отрицательная бесконечность, и вторым параметром является положительная бесконечность, то результат double оцените самый близкий к.
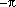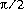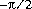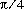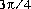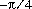Если обоими параметрами является отрицательная бесконечность, то результат double оцените самый близкий к.

20.11.10 public static double exp(double a)

Этот метод вычисляет приближение к показательной функции параметра (e возведенный в степень параметра, где e является основой натуральных логарифмов (§20.11.1)), используя exp алгоритм как публикующийся в fdlibm (см. введение в этот раздел).

Особые случаи:

Если параметром является НЭН, то результатом является НЭН.
Если параметром является положительная бесконечность, то результатом является положительная бесконечность.
Если параметром является отрицательная бесконечность, то результатом является положительный нуль.

20.11.11 public static double log(double a)

Этот метод вычисляет приближение к натуральному логарифму параметра, используя log алгоритм как публикующийся в fdlibm (см. введение в этот раздел).

Особые случаи:

Если параметром является НЭН или меньше чем нуль, то результатом является НЭН.
Если параметром является положительная бесконечность, то результатом является положительная бесконечность.
Если параметром является положительный нулевой или отрицательный нуль, то результатом является отрицательная бесконечность.

20.11.12 public static double sqrt(double a)

Этот метод вычисляет приближение к квадратному корню параметра.

Особые случаи:

Если параметром является НЭН или меньше чем нуль, то результатом является НЭН.
Если параметром является положительная бесконечность, то результатом является положительная бесконечность.
Если параметром является положительный нулевой или отрицательный нуль, то результатом является то же самое как параметр.

Иначе, результат double оцените самый близкий к истинному математическому квадратному корню значения аргумента.

20.11.13 public static double pow(double a, double b)

Этот метод вычисляет приближение к математической работе возведения в степень первого параметра второго параметра, используя pow алгоритм как публикующийся в fdlibm (см. введение в этот раздел).

Особые случаи:

Если вторым параметром является положительный или отрицательный нуль, то результат 1.0.
Если второй параметр 1.0, тогда результатом является то же самое как первый параметр.
Если вторым параметром является НЭН, то результатом является НЭН.
Если первым параметром является НЭН, и второй параметр является ненулевым, то результатом является НЭН.
Если абсолютное значение первого параметра больше чем 1, и вторым параметром является положительная бесконечность, или абсолютное значение первого параметра - меньше чем 1, и вторым параметром является отрицательная бесконечность, то результатом является положительная бесконечность.
Если абсолютное значение первого параметра больше чем 1, и вторым параметром является отрицательная бесконечность, или абсолютное значение первого параметра - меньше чем 1, и вторым параметром является положительная бесконечность, то результатом является положительный нуль.
Если абсолютное значение первого параметра равняется 1, и второй параметр бесконечен, то результатом является НЭН.
Если первым параметром является положительный нуль, и второй параметр больше чем нуль, или первым параметром является положительная бесконечность, и вторым параметром являются меньше чем нуль, то результатом является положительный нуль.
Если первым параметром является положительный нуль, и вторым параметром являются меньше чем нуль, или первым параметром является положительная бесконечность, и второй параметр больше чем нуль, то результатом является положительная бесконечность.
Если первым параметром является отрицательный нуль, и второй параметр больше чем нуль, но не конечное нечетное целое число, или первым параметром является отрицательная бесконечность, и вторым параметром являются меньше чем нуль, но не конечное нечетное целое число, то результатом является положительный нуль.
Если первым параметром является отрицательный нуль, и вторым параметром является положительное конечное нечетное целое число, или первым параметром является отрицательная бесконечность, и вторым параметром является отрицательное конечное нечетное целое число, то результатом является отрицательный нуль.
Если первым параметром является отрицательный нуль, и вторым параметром являются меньше чем нуль, но не конечное нечетное целое число, или первым параметром является отрицательная бесконечность, и второй параметр больше чем нуль, но не конечное нечетное целое число, то результатом является положительная бесконечность.
Если первым параметром является отрицательный нуль, и вторым параметром является отрицательное конечное нечетное целое число, или первым параметром является отрицательная бесконечность, и вторым параметром является положительное конечное нечетное целое число, то результатом является отрицательная бесконечность.
Если первым параметром являются меньше, чем нуль и второй параметр являются конечным даже целое число, то результат равен результату повышения абсолютного значения первого параметра питанию второго параметра.
Если первым параметром являются меньше, чем нуль и второй параметр являются конечным нечетным целым числом, то результат равен отрицанию результата повышения абсолютного значения первого параметра питанию второго параметра.
Если первый параметр конечен и меньше, чем нуль и второй параметр конечны и не целое число, то результатом является НЭН.
Если обоими параметрами являются целые числа, то результат точно равен математическому результату возведения в степень первого параметра второго параметра, если тот результат может фактически быть представлен точно как a double значение.

(В предшествующих описаниях значение с плавающей точкой, как полагают, является целым числом, если и только если это - фиксированная точка метода ceil (§20.11.15) или, который является той же самой вещью, фиксированной точкой метода floor (§20.11.16). Значение является фиксированной точкой метода с одним параметром, если и только если результат применения метода к значению равен значению.)

20.11.14 public static double IEEEremainder(double x, double y)

Этот метод вычисляет работу остатка на двух параметрах как предписано стандартом IEEE 754: значение остатка математически равно 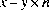туда, где математическое целое число, самое близкое к точному математическому значению частного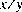; если два математических целых числа одинаково близко к 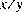тогда n, целое число, которое является даже. Если остаток является нулем, его знак является тем же самым как знаком первого параметра.

Особые случаи:

Если или параметром является НЭН, или первый параметр бесконечен, или вторым параметром является положительный нулевой или отрицательный нуль, то результатом является НЭН.
Если первый параметр конечен, и второй параметр бесконечен, то результатом является то же самое как первый параметр.

20.11.15 public static double ceil(double a)

Результат является самым маленьким (самый близкий к отрицательной бесконечности) double значение, которое не является меньше чем параметр и равно математическому целому числу.

Особые случаи:

Если значение аргумента уже равно математическому целому числу, то результатом является то же самое как параметр.
Если параметром является НЭН или бесконечность или положительный нулевой или отрицательный нуль, то результатом является то же самое как параметр.
Если значение аргумента является меньше чем нуль, но больше чем -1.0, тогда результатом является отрицательный нуль.

Отметьте что значение Math.ceil(x) точно значение -Math.floor(-x).

20.11.16 public static double floor(double a)

Результат является самым большим (самый близкий к положительной бесконечности) double значение, которое не больше чем параметр и равно математическому целому числу.

Особые случаи:

Если значение аргумента уже равно математическому целому числу, то результатом является то же самое как параметр.
Если параметром является НЭН или бесконечность или положительный нулевой или отрицательный нуль, то результатом является то же самое как параметр.

20.11.17 public static double rint(double a)

Результат double значение, которое является самым близким в значении к параметру и является равным математическому целому числу. Если два double значения, которые являются математическими целыми числами, одинаково близко к значению параметра, результатом является целочисленное значение, которое является даже.

Особые случаи:

Если значение аргумента уже равно математическому целому числу, то результатом является то же самое как параметр.
Если параметром является НЭН или бесконечность или положительный нулевой или отрицательный нуль, то результатом является то же самое как параметр.

20.11.18 public static int round(float a)

Результат округляется к целому числу, добавляя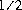, получая слово результата, и бросая результат ввести int.

Другими словами результат равен значению выражения:

(int)Math.floor(a + 0.5f)

Особые случаи:

Если параметром является НЭН, результат 0.
Если параметром является отрицательная бесконечность, или действительно какое-либо значение, меньше чем или равное значению Integer.MIN_VALUE (§20.7.1), результат равен значению Integer.MIN_VALUE.
Если параметром является положительная бесконечность, или действительно какое-либо значение, больше чем или равный значению Integer.MAX_VALUE (§20.7.2), результат равен значению Integer.MAX_VALUE.

20.11.19 public static long round(double a)

Результат округляется к целому числу, добавляя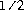, получая слово результата, и бросая результат ввести long.

Другими словами результат равен значению выражения:

(long)Math.floor(a + 0.5d)

Особые случаи:

Если параметром является НЭН, результат 0.
Если параметром является отрицательная бесконечность, или действительно какое-либо значение, меньше чем или равное значению Long.MIN_VALUE (§20.7.1), результат равен значению Long.MIN_VALUE.
Если параметром является положительная бесконечность, или действительно какое-либо значение, больше чем или равный значению Long.MAX_VALUE (§20.7.2), результат равен значению Long.MAX_VALUE.

20.11.20 public static double random()

Результатом является двойное значение с положительным знаком, больше чем или равный нулю, но меньше чем 1.0, выбранный псевдобеспорядочно с (приблизительно) равномерным распределением от того диапазона.

Когда этот метод сначала вызывают, он создает единственный новый генератор псевдослучайных чисел, точно как будто по выражению

new java.util.Random()

Этот новый генератор псевдослучайных чисел используется после того для всех звонков в этот метод и используется больше нигде.

Этот метод должным образом синхронизируется, чтобы позволить корректное использование больше чем одним потоком. Однако, если много потоков должны генерировать псевдослучайные числа по высокой цене, это может уменьшить конкуренцию для каждого потока, чтобы иметь его собственный генератор псевдослучайного числа.

20.11.21 public static int abs(int a)

Результатом является абсолютное значение параметра, если возможный.

Если параметр не отрицателен, параметр возвращается.

Если параметр отрицателен, отрицание параметра возвращается. Отметьте это, если параметр равен значению Integer.MIN_VALUE (§20.7.1), самое отрицательное представимое int значение, результатом будет та же самая отрицательная величина.

20.11.22 public static long abs(long a)

Результатом является абсолютное значение параметра, если возможный.

Если параметр не отрицателен, параметр возвращается.

Если параметр отрицателен, отрицание параметра возвращается. Отметьте это, если параметр равен значению Long.MIN_VALUE (§20.8.1), самое отрицательное представимое long значение, результатом будет та же самая отрицательная величина.

20.11.23 public static float abs(float a)

Параметр возвращается с его знаком, измененным, чтобы быть положительным.

Особые случаи:

Если параметром является положительный нулевой или отрицательный нуль, результатом является положительный нуль.
Если параметр бесконечен, результатом является положительная бесконечность.
Если параметром является НЭН, результатом является НЭН.

Другими словами результат равен значению выражения:

Float.intBitsToFloat(0x7fffffff & Float.floatToIntBits(a))

[Эта спецификация для метода abs планируется для введения в версии 1.1 Java. В предыдущих версиях Java, abs(-0.0f) возвраты -0.0f, который не корректен.]

20.11.24 public static double abs(double a)

Параметр возвращается с его знаком, измененным, чтобы быть положительным.

Особые случаи:

Если параметром является положительный нулевой или отрицательный нуль, результатом является положительный нуль.
Если параметр бесконечен, результатом является положительная бесконечность.
Если параметром является НЭН, результатом является НЭН.

Другими словами результат равен значению выражения:

Double.longBitsToDouble((Double.doubleToLongBits(a)<<1)>>>1)

[Эта спецификация для метода abs планируется для введения в версии 1.1 Java. В предыдущих версиях Java, abs(-0.0d) возвраты -0.0d, который не корректен.]

20.11.25 public static int min(int a, int b)

Результатом являются меньшие из этих двух параметров - то есть, один ближе к значению Integer.MIN_VALUE (§20.7.1). Если у параметров есть то же самое значение, результатом является то же самое значение.

20.11.26 public static long min(long a, long b)

Результатом являются меньшие из этих двух параметров - то есть, один ближе к значению Long.MIN_VALUE (§20.8.1). Если у параметров есть то же самое значение, результатом является то же самое значение.

20.11.27 public static float min(float a, float b)

Результатом являются меньшие из этих двух параметров - то есть, один ближе к отрицательной бесконечности. Если у параметров есть то же самое значение, результатом является то же самое значение.

Особые случаи:

Если одним параметром является положительный нуль, и другой отрицательный нуль, результатом является отрицательный нуль.
Если любым параметром является НЭН, результатом является НЭН.

[Эта спецификация для метода min планируется для введения в версии 1.1 Java. В предыдущих версиях Java, min(0.0f, -0.0f) возвраты 0.0f, который не корректен.]

20.11.28 public static double min(double a, double b)

Особые случаи:

Если одним параметром является положительный нуль, и другой отрицательный нуль, результатом является отрицательный нуль.
Если любым параметром является НЭН, результатом является НЭН.

[Эта спецификация для метода min планируется для введения в версии 1.1 Java. В предыдущих версиях Java, min(0.0d, -0.0d) возвраты 0.0d, который не корректен.]

20.11.29 public static int max(int a, int b)

Результатом являются большие из этих двух параметров - то есть, один ближе к значению Integer.MAX_VALUE (§20.7.2). Если у параметров есть то же самое значение, результатом является то же самое значение.

20.11.30 public static long max(long a, long b)

Результатом являются большие из этих двух параметров - то есть, один ближе к значению Long.MAX_VALUE (§20.8.2). Если у параметров есть то же самое значение, результатом является то же самое значение.

20.11.31 public static float max(float a, float b)

Результатом являются большие из этих двух параметров - то есть, один ближе к положительной бесконечности. Если у параметров есть то же самое значение, результатом является то же самое значение.

Особые случаи:

Если одним параметром является положительный нуль, и другой отрицательный нуль, результатом является положительный нуль.
Если любым параметром является НЭН, результатом является НЭН.

[Эта спецификация для метода max планируется для введения в версии 1.1 Java. В предыдущих версиях Java, max(-0.0f, 0.0f) возвраты -0.0f, который не корректен.]

20.11.32 public static double max(double a, double b)

Особые случаи:

Если одним параметром является положительный нуль, и другой отрицательный нуль, результатом является положительный нуль.
Если любым параметром является НЭН, результатом является НЭН.

[Эта спецификация для метода max планируется для введения в версии 1.1 Java. В предыдущих версиях Java, max(-0.0d, 0.0d) возвраты -0.0d, который не корректен.].

Содержание | Предыдущий | Следующий | Индекс

Спецификация языка Java (HTML, сгенерированный Блинчиком "сюзет" Pelouch 24 февраля 1998)
Авторское право © Sun Microsystems, Inc 1996 года. Все права защищены
Пожалуйста, отправьте любые комментарии или исправления к doug.kramer@sun.com

20.11 Класс java.lang.Math

20.11 Класс `java.lang.Math`