Используя преобразования Фурье
Введение
vDSP API обеспечивает преобразования Фурье для преобразования одномерных и двумерных данных между временным интервалом и частотной областью.
Массивы весов FFT
Для повышения производительности, vDSP функции, обрабатывающие данные частотной области, ожидают массив сложных экспоненциалов (иногда вызываемый, вертят факторы) существовать до вызывания функции. После того, как создаваемый, этот массив весов FFT может использоваться много раз той же функцией Фурье и может быть совместно использован несколькими функциями Фурье.
Массивы весов FFT создаются путем вызова vDSP_create_fftsetup (одинарная точность) или vDSP_create_fftsetupD (двойная точность). Прежде, чем вызвать функцию, обрабатывающую в частотной области, необходимо вызвать одну из этих функций. Вызывающая сторона указывает размер нужного массива к функции установки. Функции установки:
Создайте структуру данных для содержания массива.
Создайте массив.
Возвратите указатель на структуру данных (или
NULLесли хранение для этой структуры не могло бы быть выделено).
Указатель на структуру данных тогда передается как параметр последующим функциям Фурье. Необходимо проверить значение указателя прежде, чем предоставить указатель на функцию частотной области. Возвращенное значение нуля является единственным явным уведомлением, которое привело к сбою распределение массива.
Параметр log2n к этим функциям основа 2 логарифма n, где n число подразделений круга комплексной единицы, которые массив представляет, и таким образом указывает наибольшее число элементов, которые могут быть обработаны последующей функцией Фурье. Параметр log2n должен равняться или превысить параметр log2n предоставленный любым функциям с помощью массива весов. Когда таблица имеет больше разрешения, или больше, функции автоматически корректируют свои шаги через массив n, чем требуемый.
Таким образом, единственный вызов к vDSP_create_fftsetup или vDSP_create_fftsetupD может служить серии вызовов к функциям FFT пока n является достаточно большим для каждой вызванной функции и, пока сохраняется массив весов.
Например, если необходимо вызвать vDSP_fft_zrip для 256 точек данных необходимо вызвать vDSP_create_fftsetup с logn из по крайней мере 8. Если также необходимо вызвать vDSP_fft_zrip для ряда 2 048 точек данных, значения logn должны быть по крайней мере 11. Таким образом, Вы могли генерировать эту таблицу один раз для обоих наборов следующим образом:
FFTsetup setup; vDSP_create_fftsetup( 11, 0 ); /* supports up to 2048 (2**11) points */ |
... |
vDSP_fft_zrip( setup, small_set, 1, 8, FFT_FORWARD); /* 256 (2**8) points */ |
... |
vDSP_fft_zrip( setup, large_set, 1, 11, FFT_FORWARD); /* 2048 (2**11) points */ |
Многократное использование массива весов для столь же размерного FFTs экономично. Однако использование массива весов создало для FFT, обрабатывающего большое количество элементов, может ухудшить производительность для FFT, обрабатывающего меньшее число элементов.
Для более полного примера vDSP_create_fftsetup и функции FFT, см. vDSP Примеры.
Упаковка данных для реального FFTs
Дискретные функции преобразования Фурье в vDSP API обеспечивают уникальный случай в форматировании данных для сохранения памяти. Реальные к комплексу дискретные преобразования Фурье пишут свои выходные данные в специальных упакованных форматах так, чтобы сложный вывод не требовал больше памяти, чем реальный ввод.
Упаковка и функции трансформации
Приложениям, вызывающим реальный FFT, вероятно, придется использовать две функции трансформации, один перед вызовом FFT и один после. Если входной массив не находится в ровно-нечетной конфигурации разделения, это требуется.
Действительный массив A = {A[0],...,A[n]} должен быть преобразован в ровно-нечетный массив AEvenOdd = {A[0],A[2],...,A[n-1],A[1],A[3],...A[n]} посредством вызова vDSP_ctoz.
Результат реального FFT на AEvenOdd из размерности n сложная матрица размерности 2n, с совершенно особым форматом:
{[DC,0],C[1],C[2],...,C[n/2],[NY,0],Cc[n/2],...,Cc[2],Cc[1]}
где:
Значения
DCиNYDC и компоненты Найквиста (действительные значения)Массив
Cсложно в представлении разделенияМассив
Ccсопряженное комплексное числоCв представлении разделения
Для действительного массива A из размера n , результаты, которые сложны, требуют 2 * n пробелы. Однако большая часть этих данных является или всегда нулем или избыточна, таким образом, могут быть опущены эти данные. Таким образом, для вмещения этого результата в то же пространство как входной массив алгоритм выбрасывает эти ненужные значения. Реальный FFT хранит свои результаты следующим образом:
{[DC,NY],C[1],C[2],...,C[n/2]}.
Упаковка разделов для Одномерных Массивов и Упаковка для Двухмерных антенных решеток описывают форматы упаковки более подробно.
Упаковка для одномерных массивов
Вследствие его свойственной симметрии, прямого преобразования Фурье n вводы с плавающей точкой от временного интервала до частотной области производят n/2 + 1 уникальные сложные выводы. Поскольку точка данных n/2 - i равняется сопряженному комплексному числу точки n/2 + i, первая половина данных частоты отдельно (до и включая точку n/2 + 1) достаточно для сохранения исходной информации.
Кроме того, упаковка данных FFT использует в своих интересах факт что мнимые части первого сложного вывода (нуль элемента) и последнего сложного вывода (элемент n/2, Частота Найквиста), всегда нуль.
Это позволяет сохранить действительную часть последнего вывода, где мнимая часть первого вывода была бы. Оцененные нулю мнимые части первых и последних выводов подразумеваются.
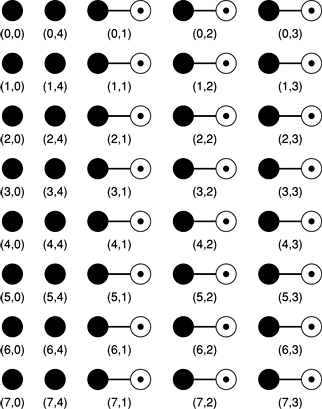
Например, рассмотрите этот действительный вектор с восемью точками, поскольку он существует до того, чтобы быть преобразованным к частотной области (рисунок 2-1).

Преобразование этих восьми основных назначений к частотной области приводит к пяти сложным значениям (рисунок 2-2).

Пять сложных значений упаковываются в выходном векторе, показанном на рисунке 2-3

Заметьте, что действительная часть вывода четыре сохранена, где мнимая часть выходного нуля была бы сохранена без упаковки. Мнимые части первого вывода и последнего вывода, всегда обнуляйте, подразумеваются.
Упаковка для двухмерных антенных решеток
Двумерные реальные к комплексу DFTs упаковываются похожим способом. При обработке двумерных реальных вводов DFTs сначала преобразовывают каждую строку и затем преобразовывают ниже на столбцы. Поскольку каждая строка преобразовывается, она упаковывается, как ранее описано для одномерных преобразований.
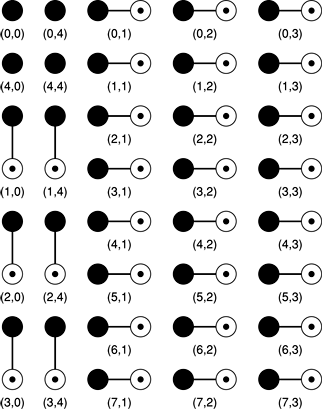
Например, для преобразования 8 8 реального изображения к частотной области сначала каждая строка преобразовывается и упаковывается как показано на рисунке 2-4
Заметьте, что каждая строка упаковывается как одномерное преобразование в более раннем примере. Упаковка приводит к 16 действительным значениям и 24 сложным значениям в в общей сложности 64 sizeof(float) ячейки памяти, размер исходной матрицы.
После того, как каждая строка обрабатывается и упаковывается, DFT тогда преобразовывает каждый столбец. Так как первая передача оставляет действительные значения в нуле столбцов и один, эти два столбца преобразовываются от реального для объединения использования того же метода упаковки вертикально, использовавшегося горизонтально на каждой строке. Таким образом преобразование этих 16 действительных значений приносит шесть сложных очков и четыре основных назначения, занимая эти 16 ячеек памяти в нуле столбцов и один.
Остающиеся три столбца сложных значений являются преобразованным от комплекса к комплексу, принося 24 сложных очка, как выведено, и требуя, чтобы 48 ячеек памяти сохранили. Это приносит общее требование хранения к 64 расположениям, размеру исходной матрицы. Завершенный 8 8 формат преобразования показан на рисунке 2-5
Масштабирование преобразований Фурье
Для обеспечения самых лучших скоростей выполнения функции vDSP библиотеки не всегда придерживаются строго формул учебника для преобразований Фурье и должны масштабироваться соответственно. Следующие разделы указывают масштабирование для каждого типа преобразования Фурье, реализованного vDSP Библиотекой. Масштабные коэффициенты также утверждаются явно в формулах, сопровождающих функциональные определения в справочной главе.
Масштабные коэффициенты получены в итоге на рисунке 2-6, показывающем реализованные значения с точки зрения математических значений. Следующие разделы описывают масштабные коэффициенты индивидуально.

Реальные преобразования Фурье
Рисунок 2-7 показывает математическую формулу для одномерного прямого преобразования Фурье.
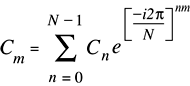
Значения коэффициентов Фурье, возвращенных реальным прямым преобразованием, как реализовано (RFимпорт), равны математическим значениям (RFматематика) времена 2:
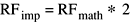
Рисунок 2-8 показывает математическую формулу для обратного преобразования Фурье.
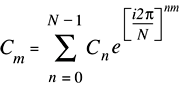
Значения коэффициентов Фурье, возвращенных реальным обратным преобразованием, как реализовано (RIимпорт), равны математическим значениям (RIматематика) времена N:
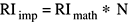
Сложные преобразования Фурье
Рисунок 2-7 показывает математическую формулу для одномерного прямого преобразования Фурье.
Значения коэффициентов Фурье, возвращенных сложным прямым преобразованием, как реализовано (CFимпорт), равны математическим значениям (CFматематика):
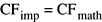
Значения коэффициентов Фурье, возвращенных сложным обратным преобразованием, как реализовано (CIимпорт), равны математическим значениям (CIматематика) времена N:
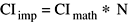
Реальные 2-мерные преобразования Фурье
Рисунок 2-9 показывает математическую формулу для 2-мерного прямого преобразования Фурье.
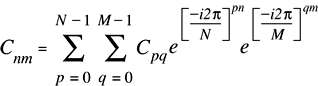
Значения коэффициентов Фурье, возвращенных 2-мерным реальным прямым преобразованием, как реализовано (RF2Dимпорт), равны математическим значениям (R2DFматематика) времена 2:
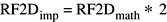
Рисунок 2-10 показывает математическую формулу для 2-мерного обратного преобразования Фурье.
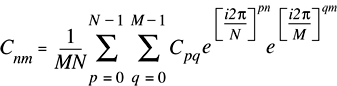
Значения коэффициентов Фурье, возвращенных 2-мерным реальным обратным преобразованием, как реализовано (RF2Dимпорт), равны математическим значениям (R2DFматематика) времена MN:
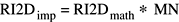
Объедините 2-мерные преобразования Фурье
Рисунок 2-9 показывает математическую формулу для 2-мерного прямого преобразования Фурье.
Значения коэффициентов Фурье, возвращенных 2-мерным сложным прямым преобразованием, как реализовано (CF2Dимпорт), равны математическим значениям (CF2Dматематика):
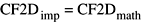
Рисунок 2-10 показывает математическую формулу для 2-мерного обратного преобразования Фурье.
Значения коэффициентов Фурье, возвращенных 2-мерным сложным обратным преобразованием, как реализовано (CI2Dимпорт), равны математическим значениям (CI2Dматематика) времена MN:
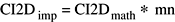
Масштабирование примера
Используя сложные двумерные преобразования как пример, при преобразовании данных от временного интервала до частотной области с vDSP_fft_zop, никакой масштабный коэффициент не представлен. Преобразование изображения от частотной области до временного интервала с vDSP_fft_zop, однако, представляет фактор N, где N векторная длина.
В следующем примере вектор преобразовывается к частотной области, обратное преобразование восстанавливает его во временном интервале, и затем это масштабируется 1/N восстановить исходный ввод (возможно, измененный погрешностями округления машины).
Перечисление 2-1 , Масштабирующее пример
~ |
~ |
scale = 1.0/((float) FFT_LENGTH) ; |
~ |
~ |
/* to the frequency domain */ |
vDSP_fft_zop( setup, |
&A, |
1, |
&B, |
1, |
FFT_LENGTH_LOG2, |
FFT_FORWARD, |
) ; |
/* back to the time domain */ |
vDSP_fft_zop( setup, |
&B, |
1, |
&A, |
1, |
FFT_LENGTH_LOG2, |
FFT_INVERSE, |
) ; |
/*scale the result */ |
vDSP_vsmul( A.realp, |
1, |
&scale, |
A.realp, |
1, |
FFT_LENGTH |
) ; |
vDSP_vsmul( A.imagp, |
1, |
&scale, |
A.imagp, |
1, |
FFT_LENGTH |
) ; |
~ |
~ |
