Преобразовывает
Кварц 2D модель получения определяет два абсолютно отдельных координатных пространства: пространство пользователя, представляющее страницу документа и пространство устройства, представляющее родное разрешение устройства. Координаты пространства пользователя являются числами с плавающей точкой, которые не связаны с разрешением пикселей в пространстве устройства. Когда Вы хотите распечатать или вывести на экран Ваш документ, Кварц отображает координаты пространства пользователя на координаты пространства устройства. Поэтому Вы никогда не должны переписывать свое приложение или писать дополнительный код для корректировки вывода из приложения для оптимального дисплея на различных устройствах.
Можно изменить пространство пользователя по умолчанию путем работы на текущую матрицу преобразования или CTM. После создания графического контекста CTM является единичной матрицей. Можно использовать Кварцевые функции трансформации, чтобы изменить CTM и, в результате изменить получение в пространстве пользователя.
Эта глава:
Обеспечивает обзор функций, которые можно использовать для выполнения трансформаций
Показывает, как изменить CTM
Описывает, как создать аффинное преобразование
Показывает, как определить, эквивалентны ли два преобразования
Описывает, как получить пользователя к пространству устройства, преобразовывают
Обсуждает математику позади аффинных преобразований
О кварцевых функциях трансформации
Можно легко перевести, масштабировать и повернуть получение с помощью Кварца 2D встроенные функции трансформации. Со всего несколькими строками кода можно применить эти трансформации в любом порядке и в любой комбинации. Рисунок 5-1 иллюстрирует эффекты масштабирования и вращения изображения. Каждая трансформация, которую Вы применяете, обновляет CTM. CTM всегда представляет текущее отображение между пространством пользователя и пространством устройства. Это отображение гарантирует, что вывод из Вашего приложения выглядит большим на любом экране дисплея или принтере.
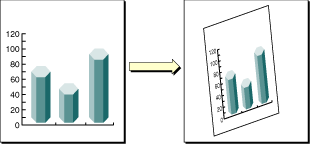
2D API Кварца обеспечивает пять функций, позволяющих Вам получать и изменять CTM. Можно повернуть, перевести и масштабировать CTM, и можно связать матрицу аффинного преобразования с CTM. Посмотрите Изменение Текущей Матрицы преобразования.
Кварц также позволяет Вам создавать аффинные преобразования, не воздействующие на пространство пользователя, пока Вы не решаете применить преобразование к CTM. Вы используете другой набор функций для создания аффинных преобразований, которые могут тогда быть связаны с CTM. Посмотрите Аффинные преобразования Создания.
Можно использовать любой набор функций, ничего не понимая о матричной математике. Однако, если Вы хотите понять то, что Кварц делает при вызове одной из функций преобразования считайте Математику Позади Матриц.
Изменение текущей матрицы преобразования
Вы управляете CTM, чтобы повернуть, масштабировать, или перевести страницу прежде, чем нарисовать изображение, таким образом преобразовывая объект, который Вы собираетесь нарисовать. Перед преобразованием CTM необходимо сохранить состояние графики так, чтобы можно было восстановить его после получения. Можно также связать CTM с аффинным преобразованием (см. Аффинные преобразования Создания). Каждая из этих четырех операций — перевод, вращение, масштабирование и связь — описаны в этом разделе вместе с функциями CTM, выполняющими каждую работу.
Следующая строка кода рисует изображение, предполагая обеспечение допустимого графического контекста, указателя на прямоугольник для рисования изображения к, и допустимый объект CGImage. Код рисует изображение, такое как демонстрационное изображение петуха, показанное на рисунке 5-2. Поскольку Вы читаете остальную часть этого раздела, Вы будете видеть, как изменения образа, поскольку Вы применяете трансформации.
CGContextDrawImage (myContext, rect, myImage); |

Перевод перемещает источник координатного пространства суммой, которую Вы указываете для осей x и y. Вы вызываете функцию CGContextTranslateCTM изменить координаты x и y каждой точки указанной суммой. Рисунок 5-3 показывает изображение, переведенное 100 модулями в оси X и 50 модулями в оси y, с помощью следующей строки кода:
CGContextTranslateCTM (myContext, 100, 50); |

Вращение перемещает координатное пространство углом, который Вы указываете. Вы вызываете функцию CGContextRotateCTM указать угол вращения, в радианах. Рисунок 5-4 показывает изображение, повернутое на-45 градусов об источнике, который является нижним левым из окна, с помощью следующей строки кода:
CGContextRotateCTM (myContext, radians(–45.)); |
Изображение отсекается, потому что вращение переместило часть изображения к расположению вне контекста. Необходимо указать угол вращения в радианах.
Если Вы планируете выполнить много вращений, полезно записать подпрограмму радианов.
#include <math.h> |
static inline double radians (double degrees) {return degrees * M_PI/180;} |

Масштабирование изменяет масштаб координатного пространства факторами x и y, которые Вы указываете, эффективно простираясь или уменьшая изображение. Величина факторов x и y управляет, больше ли новые координаты или меньше, чем оригинал. Кроме того, путем создания x факторного отрицания, можно зеркально отразить координаты вдоль оси X; точно так же можно зеркально отразить координаты горизонтально, вдоль оси y, путем создания y факторного отрицания. Вы вызываете функцию CGContextScaleCTM указать масштабные коэффициенты x и y. Рисунок 5-5 показывает изображение, значения x которого масштабируются.5 и чьи значения y масштабируются.75, с помощью следующей строки кода:
CGContextScaleCTM (myContext, .5, .75); |

Связь комбинирует две матрицы путем умножения их вместе. Можно связать несколько матриц для формирования единственной матрицы, содержащей кумулятивные эффекты матриц. Вы вызываете функцию CGContextConcatCTM объединить CTM с аффинным преобразованием. Аффинные преобразования и функции, создающие их, обсуждены в Создании Аффинных преобразований.
Другой способ достигнуть кумулятивного эффекта состоит в том, чтобы выполнить две или больше трансформации, не восстанавливая состояние графики между вызовами трансформации. Рисунок 5-6 показывает изображение, следующее из перевода изображения и затем вращения его, с помощью следующих строк кода:
CGContextTranslateCTM (myContext, w,h); |
CGContextRotateCTM (myContext, radians(-180.)); |
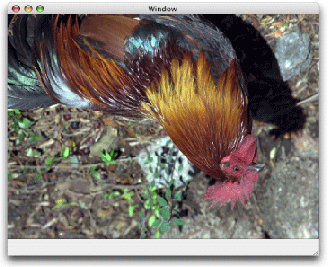
Рисунок 5-7 показывает изображение, переводящееся, масштабирующееся и поворачивающееся, с помощью следующих строк кода:
CGContextTranslateCTM (myContext, w/4, 0); |
CGContextScaleCTM (myContext, .25, .5); |
CGContextRotateCTM (myContext, radians ( 22.)); |

Порядок, в котором Вы выполняете многократные вопросы трансформаций; Вы получаете различные результаты при инвертировании порядка. Инвертируйте порядок трансформаций, используемых для создания рисунка 5-7, и Вы показали результаты на рисунке 5-8, производящемся с этим кодом:
CGContextRotateCTM (myContext, radians ( 22.)); |
CGContextScaleCTM (myContext, .25, .5); |
CGContextTranslateCTM (myContext, w/4, 0); |

Создание аффинных преобразований
Функции аффинного преобразования, доступные в Кварце, воздействуют на матрицы, не на CTM. Можно использовать эти функции для построения матрицы, что Вы позже применяетесь к CTM путем вызывания функции CGContextConcatCTM. Функции аффинного преобразования или воздействуют на, или возврат, a CGAffineTransform структура данных. Можно создать простые или сложные аффинные преобразования, которые являются допускающими повторное использование.
Функции аффинного преобразования выполняют те же операции как функции CTM — перевод, вращение, масштабирование и связь. Таблица 5-1 перечисляет функции, выполняющие эти операции вместе с информацией об их использовании. Обратите внимание на то, что существует две функции для каждого перевода, вращения и операций масштабирования.
Функция | Использовать |
|---|---|
| Создать новую матрицу перевода из значений x и y, указывающих, сколько переместить источник. |
| Применять работу перевода к существующему аффинному преобразованию. |
| Создать новую матрицу вращения из значения, указывающего в радианах, сколько повернуть систему координат. |
| Применять работу вращения к существующему аффинному преобразованию. |
| Создать новую матрицу масштабирования из значений x и y, указывающих, сколько расширить или уменьшить координаты. |
| Применять операцию масштабирования к существующему аффинному преобразованию. |
Кварц также обеспечивает функцию аффинного преобразования, инвертирующую матрицу, CGAffineTransformInvert. Инверсия обычно используется для обеспечения обратной трансформации точек в преобразованных объектах. Инверсия может быть полезной, когда необходимо восстановить значение, преобразованное матрицей: Инвертируйте матрицу и умножьте значение на инвертированную матрицу, и результатом является исходное значение. Вы обычно не должны инвертировать, преобразовывает, потому что можно инвертировать эффекты преобразования CTM путем сохранения и восстановления состояния графики.
В некоторых ситуациях Вы не могли бы хотеть преобразовывать все пространство, но просто точку или размер. Вы воздействуете на a CGPoint структура путем вызывания функции CGPointApplyAffineTransform. Вы воздействуете на a CGSize структура путем вызывания функции CGSizeApplyAffineTransform. Можно воздействовать на a CGRect структура путем вызывания функции CGRectApplyAffineTransform. Эта функция возвращает наименьший прямоугольник, содержащий преобразованные угловые точки прямоугольника, переданного ей. Если аффинное преобразование, воздействующее на прямоугольник, выполняет только масштабирование и операции перевода, возвращенный прямоугольник совпадает с прямоугольником, созданным из четырех преобразованных углов.
Можно создать новое аффинное преобразование путем вызывания функции CGAffineTransformMake, но в отличие от других функций, делающих новые аффинные преобразования, этот требует, чтобы Вы предоставили матричные записи. Для эффективного использования этой функции у Вас должно быть понимание матричной математики. Посмотрите Математику Позади Матриц.
Оценка аффинных преобразований
Можно определить, равно ли одно аффинное преобразование другому путем вызывания функции CGAffineTransformEqualToTransform. Эта функция возвраты true если эти два преобразовывают, передал ему, равны и false иначе.
Функция CGAffineTransformIsIdentity полезная функция для проверки, является ли преобразование идентификационными данными, преобразовывают. Идентификационные данные преобразовывают, не выполняет перевода, масштабирования или вращения. Применение этого преобразования к входным координатам всегда возвращает входные координаты. Постоянный Кварц CGAffineTransformIdentity представляет идентификационные данные, преобразовывают.
Получение пользователя к пространству устройства преобразовывает
Обычно, когда Вы рисуете с 2D Кварцем, Вы работаете только в пространстве пользователя. Кварц заботится о преобразовании между пространством пользователя и пространством устройства для Вас. Если Ваше приложение должно получить аффинное преобразование, что Кварцевое использование для преобразования между пространством пользователя и пространством устройства можно вызвать функцию CGContextGetUserSpaceToDeviceSpaceTransform.
Кварц обеспечивает много функций удобства для преобразования следующих конфигураций между пространством пользователя и пространством устройства. Вы могли бы счесть эти функции проще использовать, чем применение аффинного преобразования возвратилось из функции CGContextGetUserSpaceToDeviceSpaceTransform.
Точки. Функции
CGContextConvertPointToDeviceSpaceиCGContextConvertPointToUserSpaceпреобразуйте aCGPointтип данных от одного пространства до другого.Размеры. Функции
CGContextConvertSizeToDeviceSpaceиCGContextConvertSizeToUserSpaceпреобразуйте aCGSizeтип данных от одного пространства до другого.Прямоугольники. Функции
CGContextConvertRectToDeviceSpaceиCGContextConvertRectToUserSpaceпреобразуйте aCGRectтип данных от одного пространства до другого.
Математика позади матриц
Единственный Кварц 2D функция, для которой Вам нужно понимание матричной математики, является функцией CGAffineTransformMake, который делает аффинное преобразование из шести критических записей в 3 x 3 матрицами. Даже если Вы никогда не планируете создать матрицу аффинного преобразования с нуля, Вы могли бы счесть математику позади функций преобразования интересной. В противном случае можно пропустить остальную часть этой главы.
Шесть критических значений 3 x 3 матрицы преобразования — a, b, c, d, tx и ty — показаны в следующей матрице:

Учитывая 3 x 3 матрицы преобразования описали выше, Кварц использует это уравнение для преобразования точки (x, y) в результирующую точку (x’, y’):
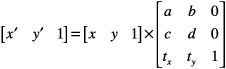
Результат находится в различной системе координат, та, преобразованная значениями переменных в матрицу преобразования. Следующие уравнения являются определением предыдущего матричного преобразования:
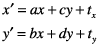
Следующая матрица является единичной матрицей. Это не выполняет перевода, масштабирования или вращения. Умножение этой матрицы входными координатами всегда возвращает входные координаты.

Используя формулы, обсужденные ранее, Вы видите, что эта матрица генерировала бы новую точку (x’, y’), который совпадает со старой точкой (x, y):
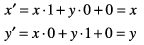
Эта матрица описывает работу перевода:
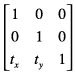
Это получающиеся уравнения что Кварцевое использование для применения перевода:
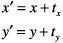
Эта матрица описывает операцию масштабирования на точке (x, y):

Это получающиеся уравнения что Кварцевое использование для масштабирования координат:
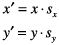
Эта матрица описывает работу вращения, поворачивая точку (x, y) против часовой стрелки углом a:

Это получающиеся уравнения что Кварцевое использование для применения вращения:
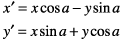
Это уравнение связывает работу вращения с работой перевода:
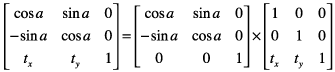
Это получающиеся уравнения что Кварцевое использование для применения преобразования:
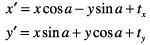
Обратите внимание на то, что порядок, в котором Вы связываете матрицы, важен — умножение матриц не является коммутативным. Т.е. результат умножения матрицы матрицей B не обязательно равняется результату умножения матрицы B матрицей A.
Как ранее упомянуто, связь является причиной, матрица аффинного преобразования содержит третий столбец с постоянными значениями 0, 0, 1. Для умножения одной матрицы против другой матрицы число столбцов одной матрицы должно соответствовать число строк другого. Это означает, что 2 x 3 матрицы не могут быть умножены против 2 x 3 матрицы. Таким образом нам нужен дополнительный столбец, содержащий постоянные значения.
Работа инверсии производит исходные координаты из преобразованных. Учитывая координаты (x, y), которые были преобразованы данным, матрицируют к новым координатам (x’, y’), преобразовывая координаты (x’, y’) инверсией матрицы A производит исходные координаты (x, y). Когда матрица умножается на ее инверсию, результатом является единичная матрица.
