Что такое шифрование?

Шифрование является трансформацией данных в форму, в которой это не может быть понято без использования некоторого ключа. Такие преобразованные данные упоминаются как шифрованный текст. Использование ключа, чтобы инвертировать этот процесс и возвратить данные его оригиналу (открытый текст или простой текст) форма вызывают дешифрованием. Большая часть безопасности APIs в OS X и iOS полагается до некоторой степени на шифрование текста или данных. Например, шифрование используется в создании сертификатов и цифровых подписей в безопасном хранении секретов в цепочке для ключей, и в безопасном транспорте информации.

Шифрование может быть чем-либо от простого процесса заменения одним символом для другого — когда ключ является правилом замены — к сложному математическому алгоритму. В целях безопасности, чем более трудный это должно дешифровать шифрованный текст, тем лучше. С другой стороны, если алгоритм слишком сложен, берет слишком долго, чтобы сделать или требует ключей, которые являются слишком большими для хранения легко, это становится непрактичным для использования в персональном компьютере. Поэтому некоторый баланс должен быть достигнут между силой шифрования (т.е. насколько трудный это для кого-то для обнаружения алгоритма и ключа), и простота использования.

Практически, шифрование только должно быть достаточно сильным для защиты данных для количества времени, данные могли бы быть полезны для лица со злонамеренным намерением. Например, если необходимо сохранить предложение на секрете договора только, пока договор не был заключен, метод шифрования, который может быть прерван, несколько недель будут достаточны. При защите номера кредитной карты Вы, вероятно, хотите метод шифрования, который не может много лет повреждаться.

Типы шифрования

Существует два основных типа шифрования в использовании в компьютерной безопасности, называемой шифрованием с симметричным ключом и шифрованием с асимметричным ключом. Тесно связанный процесс к шифрованию, в которое данные преобразовываются с помощью ключа и математического алгоритма, который не может быть инвертирован, вызывают криптографическим хешированием. Остаток от этого раздела обсуждает ключи шифрования, ключевые обменные механизмы (включая Обмен ключами Диффи-Хеллмана, используемый в некоторых безопасных транспортных протоколах), и криптографические хеш-функции.

Асимметричные ключи

В асимметричной ключевой криптографии различные ключи используются для шифрования и дешифрования сообщения. Алгоритмы с асимметричным ключом, которые являются самыми полезными, являются теми, в которых никакой ключ не может быть выведен из другого. В этом случае, в то время как другой сохранен безопасным, один ключ может быть обнародован. Это расположение часто упоминается как шифрование с открытым ключом и обеспечивает некоторые явные преимущества по симметричному шифрованию: необходимость распределения секретных ключей к большим количествам пользователей устраняется, и алгоритм может использоваться для аутентификации, а также для криптографии.

Первый алгоритм с открытым ключом, который станет широко доступным, был описан Роном Ривестом, Ади Шамиром и Леном Адлеменом в 1977, и известен как шифрование RSA от их инициалов. Несмотря на то, что другие алгоритмы с открытым ключом были созданы с тех пор, RSA все еще обычно используется. Математика метода выходит за рамки этого документа и доступна в Интернете и во многих книгах по криптографии. Алгоритм основывается на математическом манипулировании двумя большими простыми числами и их продуктом. Его сила, как полагают, связана с трудностью факторинга очень большое количество. С текущей и обозримой скоростью современных компьютеров выбором достаточно долго простые числа в генерации ключей RSA должны сделать этот алгоритм безопасным неопределенно. Однако эта вера не была доказана математически, и или быстрый алгоритм факторизации или полностью различный способ повредить шифрование RSA могли бы быть возможными. Кроме того, если практические квантовые компьютеры будут разработаны, то большие количества факторинга больше не будут тяжелой проблемой.

Другие алгоритмы с открытым ключом, на основе различной математики эквивалентной сложности к RSA, включают шифрование ElGamal и шифрование эллиптической кривой. Их использование подобно шифрованию RSA (хотя математика позади них отличается), и они не будут обсуждены далее в этом документе.

Чтобы видеть, как алгоритмы с открытым ключом решают проблему ключевого распределения, предположите, что Элис хочет получить безопасную коммуникацию от Боба. Процедура проиллюстрирована на рисунке 1-1.

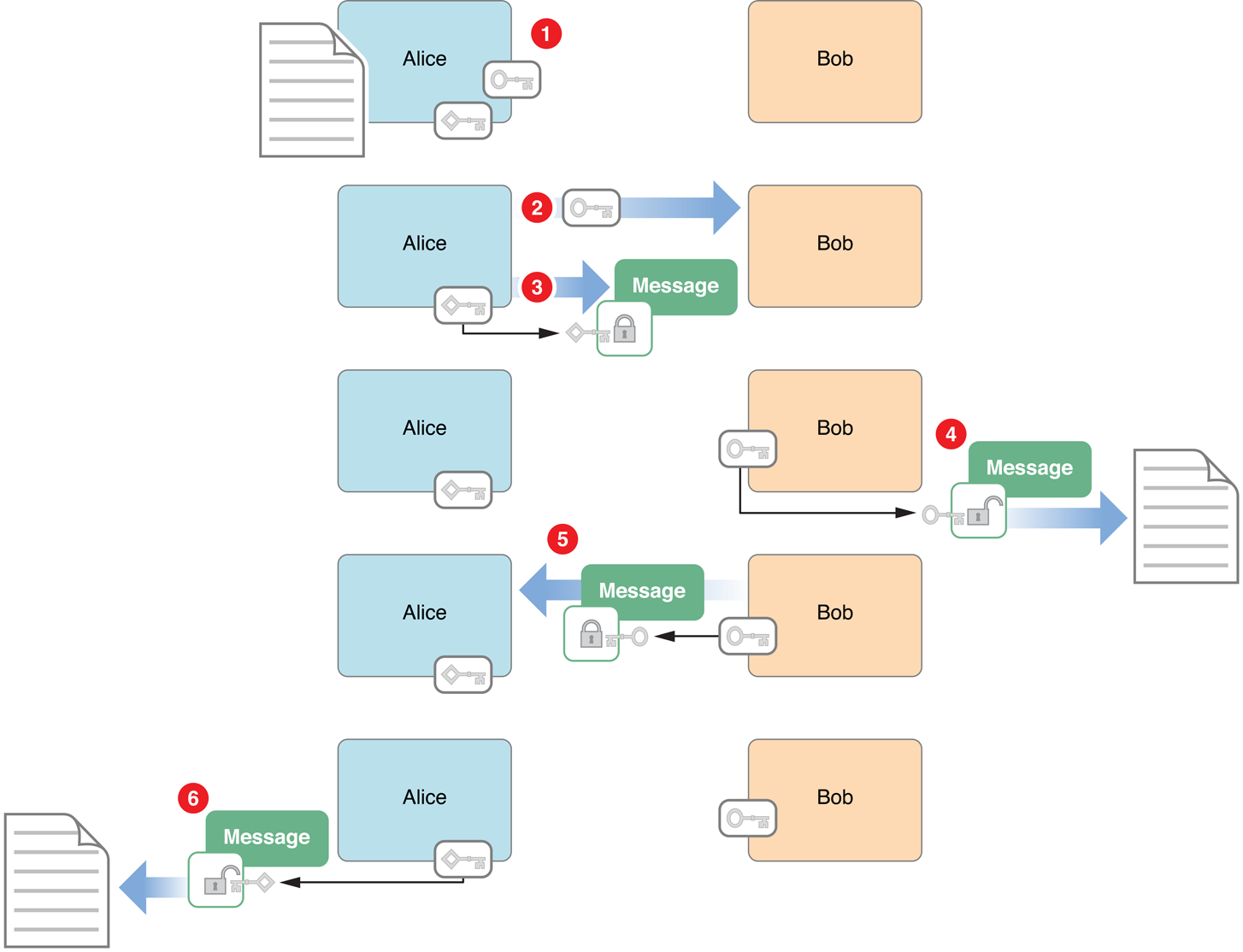
Безопасный обмен сообщениями, проиллюстрированный на рисунке 1-1, имеет следующие шаги:

1. Элис использует один из алгоритмов с открытым ключом для генерации пары ключей шифрования: закрытый ключ, который она держит в секрете, и открытый ключ. Она также подготавливает сообщение для отправки Бобу.

2. Элис отправляет открытый ключ Бобу, незашифрованному. Поскольку ее закрытый ключ не может быть выведен из открытого ключа, делание так не ставит под угрозу ее закрытый ключ всегда.

3. Элис может теперь легко удостоверить свою личность Бобу (процесс, известный как аутентификация). Для этого она шифрует свое сообщение (или любая часть сообщения) использование ее закрытого ключа и отправляет его Бобу.

4. Боб дешифрует сообщение с открытым ключом Элис. Это доказывает, что сообщение, должно быть, прибыло от Элис, поскольку только ей использовали закрытый ключ для шифрования его.

5. Боб шифрует свое сообщение с помощью открытого ключа Элис и отправляет его Элис. Сообщение безопасно, потому что, даже если оно прерывается, ни у кого, но Элис нет закрытого ключа, должен был дешифровать его.

6. Элис дешифрует сообщение со своим закрытым ключом.

Так как шифрование и аутентификация являются очень интересными предметами в национальной безопасности и защите корпоративных секретов, некоторые чрезвычайно умные люди заняты и созданием защищенных систем и попыткой повредить их. Поэтому это не должно удивлять, что фактическая безопасная коммуникация и процедуры аутентификации значительно более сложны, чем та, просто описанная. Например, метод аутентификации шифрования сообщения с Вашим закрытым ключом может обойтись атакой «человек посередине», в которой кто-то со злонамеренным намерением (обычно называемый Ив в книгах по криптографии) прерывает исходное сообщение Элис и заменяет его их собственным, так, чтобы Боб использовал не открытый ключ Элис, но Ив. Ив тогда прерывает каждое из сообщений Элис, дешифрует его с открытым ключом Элис, изменяет его (если она желает), и повторно шифрует его с ее собственным закрытым ключом. Когда Боб получает сообщение, он дешифрует его с открытым ключом Ив, думая, что ключ прибыл от Элис.

Несмотря на то, что это - предмет, слишком широкий и технический, чтобы быть покрытым подробно в этом документе, цифровые сертификаты и цифровые подписи могут помочь адресовать эти проблемы безопасности. Эти методы описаны далее в этой главе.

Обмен ключами Диффи-Хеллмана

Протокол Обмена ключами Диффи-Хеллмана является путем к двум концам сеанса связи для генерации совместно используемого симметричного ключа надежно по незащищенному каналу. Diffie-Hellman обычно реализуется с помощью математики, подобной шифрованию открытого ключа RSA. Однако подобный метод может также использоваться с шифрованием эллиптической кривой. Основные шаги упоминаются ниже:

1. Элис и Боб обмениваются открытыми ключами.

   • Для RSA эти ключи должны иметь ту же часть по модулю, p.

   • Для шифрования эллиптической кривой должны быть согласованы доменные параметры, используемые для шифрования.

   Как правило необходимо использовать или доменные значения параметров по модулю, указанные в RFC 5114.

2. Элис и Боб, каждый шифрует совместно используемое, несекретное значение, g, с помощью их закрытых ключей, и они обмениваются этими зашифрованными значениями.

   Значение для g также обычно принимается от RFC 5114, но если другое значение выбрано при использовании RSA, значение для g должно быть модификацией первообразного корня p — т.е. любое число, не совместно использующее общих делителей с p кроме 1, является конгруэнтным питанию g модификации p.

3. Элис шифрует зашифрованное значение, полученное от Боба с ее закрытым ключом, и наоборот. Эти значения используются в качестве совместно используемого сеансового ключа.

В этой точке, даже при том, что никакая сторона не знает закрытого ключа другой стороны, сеансовые ключи обеих сторон идентичны. Третье лицо, прерывающее открытые ключи, но испытывающее недостаток в знании любого закрытого ключа, не может генерировать сеансовый ключ. Поэтому данные, зашифрованные с получающимся сеансовым ключом, безопасны в то время как в пути.

Несмотря на то, что Обмен ключами Диффи-Хеллмана обеспечивает надежную защиту против компромисса прерванных данных, это не обеспечивает механизма для обеспечения, что объект на другом конце соединения - то, кто Вы думаете, что это. Т.е. этот протокол уязвим для атаки «человек посередине». Поэтому это иногда используется вместе с некоторым другим методом аутентификации гарантировать целостность данных.

Обмен ключами Диффи-Хеллмана поддерживается версией 3.1 файлового протокола Apple (AFP) и позже и Безопасным Транспортным API Apple. Поскольку шифрование RSA имеет тенденцию быть медленнее, чем методы симметричного ключа, Diffie-Hellman (и другие системы, где открытые ключи используются для генерации симметричных закрытых ключей) может быть полезным, когда нужно обменяться большим количеством зашифрованных данных.

Криптографические хеш-функции

Криптографическая хеш-функция берет любой объем данных и применяет алгоритм, преобразовывающий его в выходное значение фиксированного размера. Для криптографической хеш-функции, чтобы быть полезным, это должно быть чрезвычайно трудно или невозможно восстановить исходные данные от значения хэш-функции, и должно быть крайне маловероятно, что то же выходное значение могло следовать из любых других входных данных.

Иногда более важно проверить целостность данных, чем держать его в секрете. Например, если бы Элис отправила сообщение Бобу, дающему ему команду раскромсать некоторые записи (по закону, конечно), то для Боба было бы важно проверить, что список документов был точен перед продолжением измельчения. Так как измельчение законно, однако, нет никакой потребности зашифровать сообщение, в вычислительном отношении дорогой и длительный процесс. Вместо этого Элис могла вычислить хеш сообщения (названный дайджестом сообщения) и зашифровать обзор с ее закрытым ключом. Когда Боб получает сообщение, он дешифрует дайджест сообщения с открытым ключом Элис (таким образом проверяющий, что сообщение от Элис), и вычисляет его собственный дайджест сообщения из текста сообщения. Если эти два обзора соответствуют, Боб знает, что сообщение не повредили или вмешались.

Наиболее распространенная хеш-функция, которую Вы будете использовать, является SHA 1, алгоритм, разработанный и опубликованный правительством США, производящим 160-разрядное значение хэш-функции из любых данных до 2 ** 64 бита в длине. Существует также много более экзотических алгоритмов, таких как SHA 2, основанные на эллиптической кривой алгоритмы, и т.д.

Для совместимости с существующими системами и инфраструктурой, Вы, возможно, иногда должны использовать более старые алгоритмы, такие как MD5, но им не рекомендуют для использования в новых проектах из-за известных слабых мест.

Цифровые подписи

Цифровые подписи являются способом гарантировать целостность сообщения или других данных с помощью шифрования с открытым ключом. Как традиционные подписи, записанные с чернилами на бумаге, они могут использоваться для аутентификации идентификационных данных подписывающего лица данных. Однако цифровые подписи идут вне традиционных подписей, в которых они могут также гарантировать, что не были изменены сами данные. Это походит на подписание регистрации такого способа, которым, если кто-то изменяет сумму суммы, записанной на проверке, «Недопустимый» штамп становится видимым на поверхности проверки.

Прежде чем подписывающее лицо может создать цифровую подпись, у подписывающего лица должны сначала быть цифровые идентификационные данные — пара общедоступная с закрытым ключом и соответствующий цифровой сертификат, доказывающий подлинность открытого ключа подписывающего лица.

Подписывающее лицо генерирует дайджест сообщения данных и затем использует закрытый ключ для шифрования обзора. Подписывающее лицо включает зашифрованный обзор и информацию о цифровом сертификате подписывающего лица вместе с сообщением. Комбинация зашифрованного обзора и цифрового сертификата является цифровой подписью.

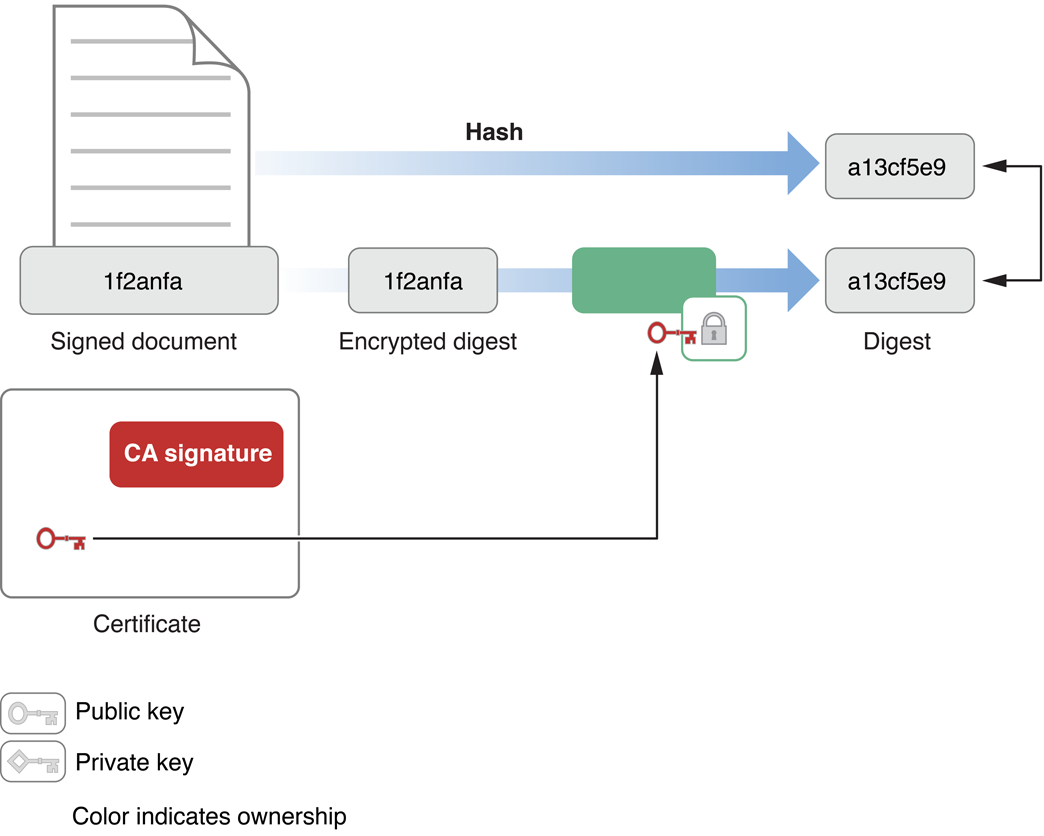
Сертификат может позже использоваться получателем для заверения подписи; сертификат включает открытый ключ, должен был дешифровать обзор, и алгоритм раньше создавал обзор. Чтобы проверить, что подписанный документ не был изменен, получатель использует тот же алгоритм для создания обзора сообщения, как получено, затем использует открытый ключ для дешифрования зашифрованного обзора от подписи сообщения. Если эти два обзора идентичны, то сообщение не могло быть изменено и, должно быть, было отправлено владельцем открытого ключа.

Чтобы гарантировать что лицо кто, если подпись не является только тем же лицом, которое предоставило данные, но и является также, кем он или она утверждает, что был, сертификат также подписывается — в этом случае центром сертификации, кто выпустил сертификат. (Больше на центрах сертификации позже.)

Цифровые подписи играют ключевую роль в подписывании кода. Разработчики призваны подписать свои приложения. На выполнении подпись каждого приложения проверяется на законность. Цифровые подписи требуются на всех приложениях для iOS. Считайте Руководство по Подписыванию кода для подробных данных о том, как подписывание кода используется OS X и iOS.

Рисунок 1-2 иллюстрирует создание цифровой подписи.

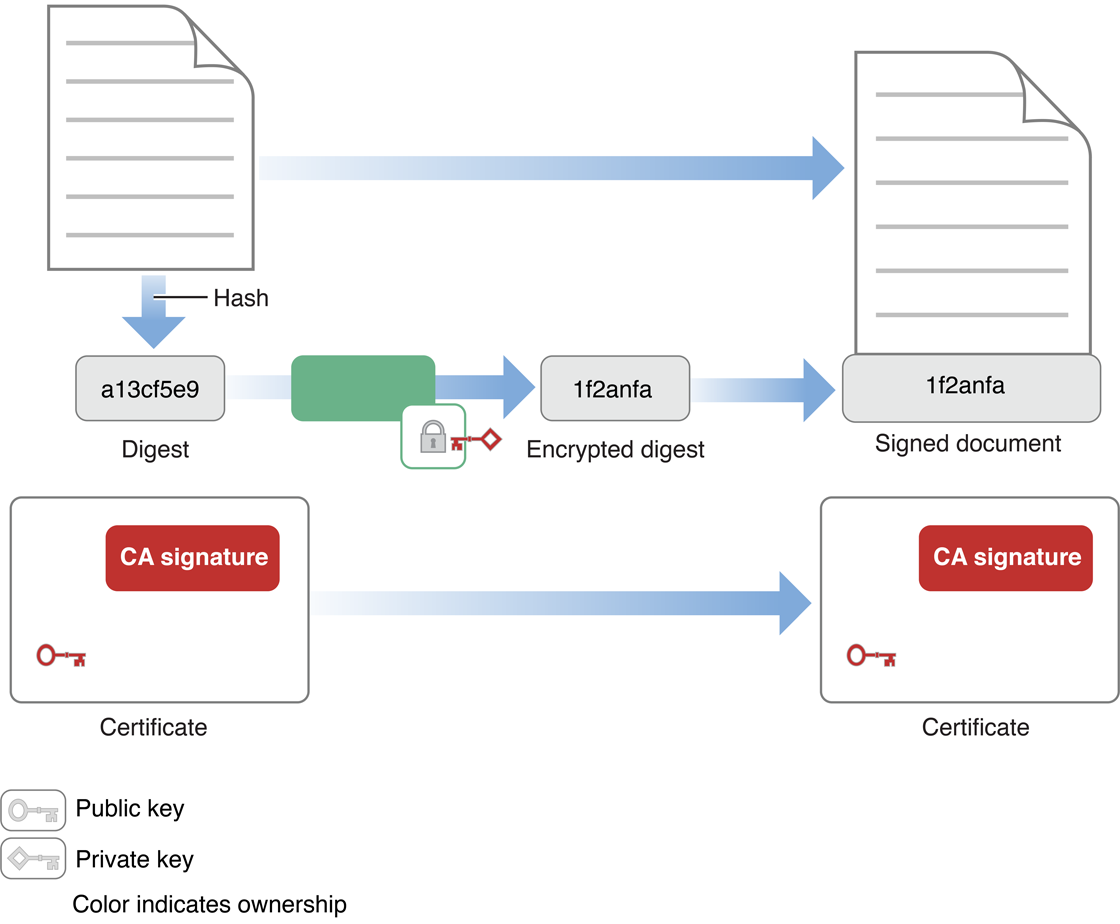
Рисунок 1-3 иллюстрирует проверку цифровой подписи. Получатель получает открытый ключ подписывающего лица из сертификата и использования подписывающего лица что дешифровать обзор. Затем с помощью алгоритма, обозначенного в сертификате, получатель создает новый обзор данных и сравнивает новый обзор с дешифрованной копией той, поставленной в подписи. Если они соответствуют, то полученные данные должны быть идентичны исходным данным, создаваемым подписывающим лицом.

Цифровые сертификаты

Цифровой сертификат является набором данных, используемых для проверки идентификационных данных держателя или отправителя сертификата.

Например, сертификат X.509 содержит такую информацию как:

• Структурная информация — версия, порядковый номер, алгоритм выборки сообщений раньше создавал подпись и т.д.

• Цифровая подпись от центра сертификации (CA) — лицо или организация, выпустившая сертификат — чтобы гарантировать, что сертификат не был изменен и указать идентификационные данные эмитента

• Информация о владельце сертификата — имя, адрес электронной почты, название компании, открытый ключ владельца, и т.д.

• Срок действия (сертификат не допустим прежде или после этого периода),

• Расширения сертификата — атрибуты, содержащие дополнительную информацию, такую как допустимое использование для этого сертификата

Осторожный читатель заметит, что цифровая подпись включает сертификат о подписывающем лице, и что сертификат подписывающего лица, в свою очередь, содержит цифровую подпись, включающую другой сертификат.

В целом каждый сертификат проверяется с помощью другого сертификата, создавая цепочку доверия — цепочка сертификатов, каждый из которых снабжен цифровой подписью следующим сертификатом в цепочке, заканчивающейся корневым сертификатом. Владельца этого корневого сертификата вызывают корневым центром сертификации. Рисунок 1-4 иллюстрирует части цифрового сертификата.

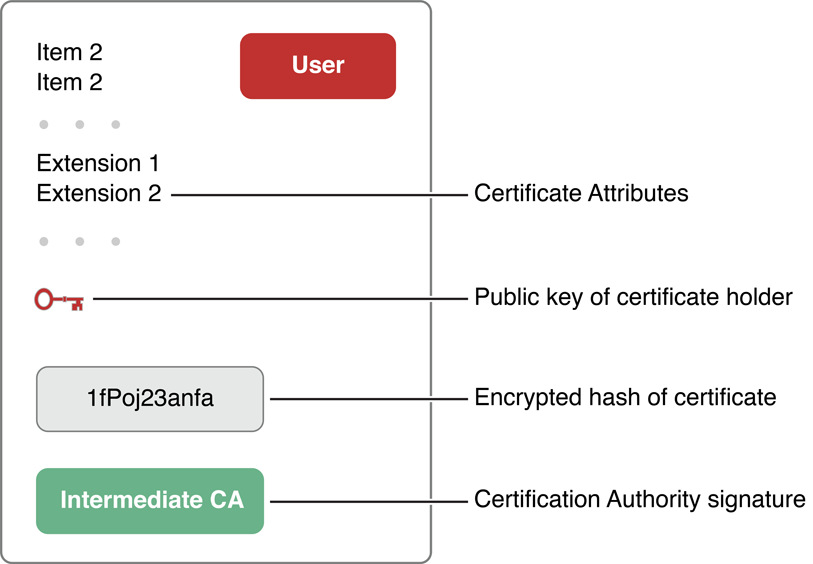
Корневой сертификат самоподписывается, означая, что подпись корневого сертификата создавалась полностью центр сертификации самостоятельно. Рисунок 1-5 и рисунок 1-6 иллюстрируют, как цепочка сертификатов создается и используется. Рисунок 1-5 показывает, как корневой центр сертификации создает свой собственный сертификат и затем создает сертификат для вторичного центра сертификации.

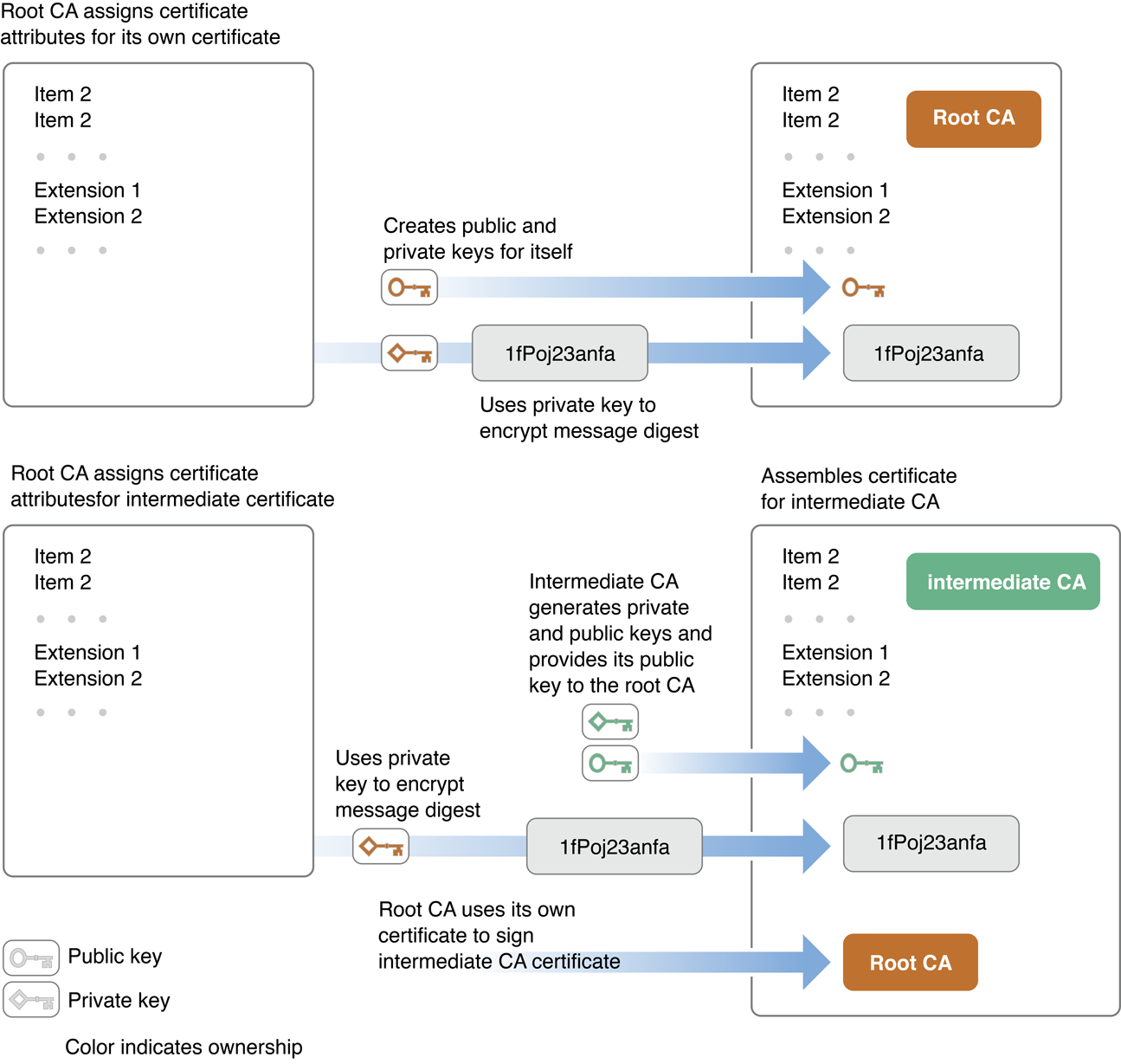
Рисунок 1-6 показывает, как вторичный центр сертификации создает сертификат для конечного пользователя и как конечный пользователь использует его для подписания документа.

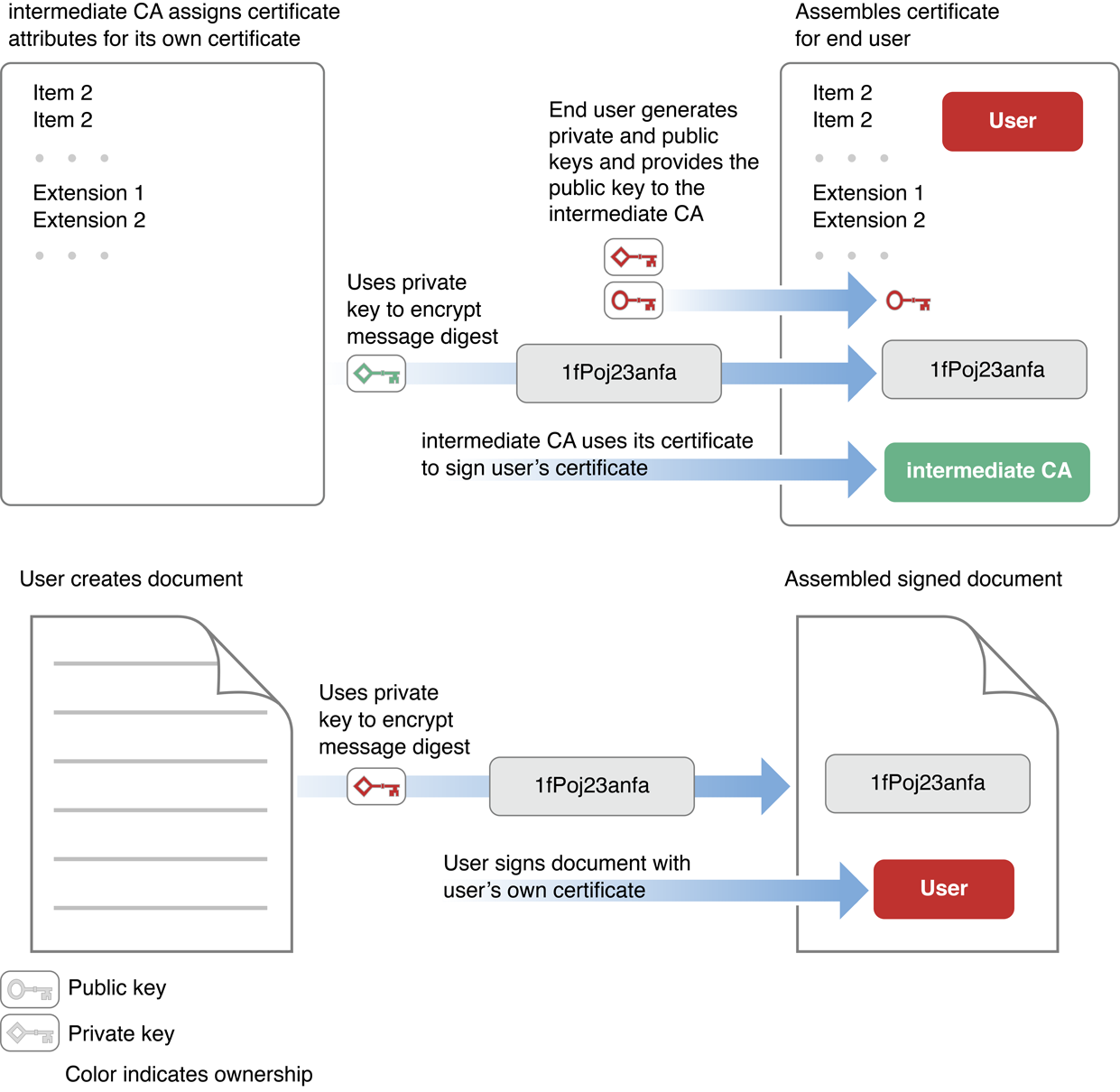
На рисунке 1-6 создатель документа подписал документ. Подпись указывает сертификат о создателе документа (маркированный Пользователь в числе). Создатель документа подписывает документ с закрытым ключом, и сертификат подписания содержит соответствующий открытый ключ, который может использоваться для дешифрования дайджеста сообщения для заверения подписи (описанный ранее в Цифровых подписях). Этот сертификат — вместе с закрытыми и открытыми ключами — был предоставлен центром сертификации (CA).

Для проверки законности сертификата пользователя сертификат подписывается с помощью сертификата о Приблизительно, сертификат о CA включает открытый ключ, должен был дешифровать дайджест сообщения сертификата пользователя. Продолжая цепочку сертификата, сертификат о CA подписывается с помощью сертификата о полномочиях, кто выпустил тот сертификат. Цепочка может продолжиться через любое число промежуточных сертификатов, но на рисунке 1-5 эмитент сертификата CA является корневым центром сертификации. Обратите внимание на то, что сертификат о корневом CA, в отличие от других, самоподписывается — т.е. он не относится к дальнейшему центру сертификации, но подписывается с помощью собственного закрытого ключа корневого CA.

Когда CA создает сертификат, он использует свой закрытый ключ для шифрования дайджеста сообщения сертификата. Подпись каждого сертификата проблемы CA обращается к его собственному сертификату подписания. Открытый ключ CA находится в этом сертификате, и приложение, заверяющее подпись, должно извлечь этот ключ для проверки сертификата о Приблизительно, Таким образом, это продолжается, на вниз цепочке сертификата, к сертификату о корне Приблизительно, Когда корневой CA выпускает сертификат, это, также, подписывает сертификат. Однако этот сертификат подписания не был выпущен другим CA; цепочка останавливается здесь. Скорее корневой CA выпускает его собственный сертификат подписания, как показано на рисунке 1-5.

Сертификат о корневом CA может быть проверен путем создания обзора и сравнения его с одним широко доступным. Как правило, корневой сертификат и открытый ключ корневого CA уже сохранены в приложении или на компьютере, который должен заверить подпись.

Возможно закончить цепочку сертификата доверяемым сертификатом, который не является корневым сертификатом. Например, сертификат может сертифицироваться, как доверял пользователь или может быть перекрестный сертифицируемый — т.е. подписанный больше чем с одной цепочкой сертификата. Общий термин для сертификата доверял, чтобы сертифицировать, что другие сертификаты — включая корневые сертификаты и других — являются сертификатом привязки. Поскольку большинство сертификатов привязки является корневыми сертификатами, два термина часто используются взаимозаменяемо.

Уверенность, которую Вы можете иметь в данном сертификате, зависит от уверенности, которую Вы имеете в сертификате привязки; например, доверие, которое Вы имеете в центрах сертификации и в их процедурах для обеспечения, что полностью аутентифицируются последующие получатели сертификата в цепочке сертификата. Поэтому это всегда - хорошая идея исследовать сертификат, идущий с цифровой подписью, даже когда подпись, кажется, допустима. В OS X и iOS, все сертификаты, которые Вы получаете, сохранены в Вашей цепочке для ключей. В OS X можно использовать утилиту Keychain Access для просмотра их.

Определенные атрибуты цифрового сертификата (известный как расширения сертификата) предоставляют дополнительную информацию о сертификате. Некоторые из этих расширений описывают, как сертификат был предназначен, чтобы использоваться. Например, расширение сертификата могло бы указать, что ключ может использоваться для подписывания кода или мог бы обеспечить список дополнительных доменных имен, для которых сертификат TLS допустим. Другие расширения обеспечивают подписанные метки времени, указывающие, когда сертификат использовался для подписания определенного документа, таким образом позволяя Вам проверить, что теперь истекший сертификат был допустим, когда это использовалось для подписания документа. Все еще другие предоставляют информацию, используемую для проверки, был ли отменен сертификат. И т.д.

Эти расширения сертификата интерпретируются в контексте доверительной политики — ряд правил, которые указывают, как определенное расширение влияет, нужно ли сертификату доверять для данного использования. Например, доверительная политика могла бы указать, что для доверия для проверки снабженного цифровой подписью электронного письма, сертификат должен содержать адрес электронной почты, соответствующий адрес отправителя электронной почты.