Настройка производительности на GPU
GPUs и CPUs имеют существенно различную архитектуру и тем самым потребуйте различной оптимизации для OpenCL. CPU имеет относительно небольшое количество обработки элементов и большого объема памяти (и большой кэш и намного большая сумма RAM, доступного на печатной плате). GPU имеет относительно большое количество обработки элементов и обычно имеет меньше памяти, чем CPU. Поэтому код, работающий самый быстрый на GPU, будет разработан, чтобы привести меньше памяти в рабочее состояние и использовать в своих интересах GPU’s превосходящая вычислительная мощность. Кроме того, доступ к памяти GPU быстр, когда схема доступа соответствует архитектуру памяти, таким образом, код должен быть разработан с этим в памяти.
Возможно записать код OpenCL, который может работать эффективно и на CPU и на GPU. Однако для получения оптимальной производительности обычно необходимо записать различный код для каждого типа устройства.
Эта глава фокусируется о том, как улучшить производительность относительно GPU. Это начинается путем описания значительных повышений производительности на GPU, который может быть получен посредством настройки (см., Почему Необходимо Настроиться), APIs списков, который можно использовать для выполнения временного кода (см. Измеряющую Производительность На Устройствах), описывают, как можно оценить оптимальную производительность устройств GPU (см. Генерацию Вычислить/Доступ к памяти Пикового Сравнительного теста), описывает протокол, который может сопровождаться для настройки производительности GPU (см. Настраивающуюся Процедуру), затем продвигается через пример, в котором получено повышение производительности. (См. Улучшающуюся Производительность На CPU для предложений для оптимизации производительности на CPU.) Посмотрите Таблицу 14-1 в конце главы для обычно применимых предложений для измерения и улучшения производительности на большей части GPUs.
Почему необходимо настроиться
Настройка Вашего кода OpenCL для GPU может привести к двум - к десятикратному улучшению производительности. Рисунок 14-1 иллюстрирует типичные улучшения скорости обработки, полученной, когда было оптимизировано приложение, выполняющее Гауссову размытость на 16 изображениях MP. Процесс, сопровождаемый для оптимизации этого кода, описан в Примере: Настройка Производительности Гауссовой Размытости.
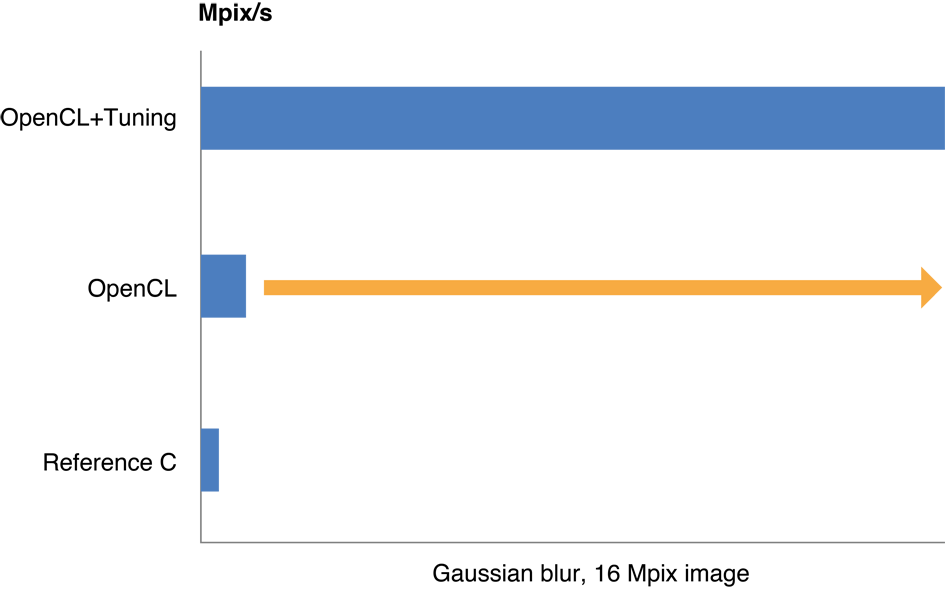
Прежде, чем оптимизировать код
Прежде чем Вы решите оптимизировать код:
-
Решите, должен ли действительно быть оптимизирован код. Оптимизация может занять время и усилие. Взвесьте затраты и преимущества оптимизации прежде, чем запустить любое усилие по оптимизации.
-
Оцените оптимальную производительность. Выполните некоторые простые ядра на своем устройстве GPU для оценки его возможностей. Можно использовать методы, описанные в Измерении Производительности На Устройствах для измерения, сколько времени код ядра берет для выполнения. Посмотрите Генерацию Вычислить/Доступ к памяти Пикового Сравнительного теста для примеров кода, который можно использовать для тестирования скорости доступа к памяти и скорости обработки.
Генерируйте или соберите демонстрационные данные для питания посредством каждой итерации оптимизации. Выполните неоптимизированный исходный код через пример кода и сохраните результаты. Тогда выполните каждую основную итерацию оптимизированного кода против тех же данных и сравните результаты с исходными результатами гарантировать, что Ваш вывод не был поврежден измененным кодом.
Измерение производительности на устройствах
Точка оптимизации приложения OpenCL должна заставить его работать быстрее. На каждом шаге процесса оптимизации необходимо знать, как быстро оптимизированный код берет для выполнения. Определить, сколько времени требуется ядро для выполнения:
Запустите таймер перед вызовом ядра:
cl_timer gcl_start_timer(void);Вызовите эту функцию для запуска таймера. Это возвращает a
cl_timerто, что Вы используете для остановки таймера.Остановите таймер сразу после возвратов ядра:
double gcl_stop_timer(cl_timer timer);Вызовите эту функцию для остановки таймера, создаваемого, когда Вы вызвали
gcl_start_timerфункция. Это возвращает прошедшее время в секундах начиная с вызова кcl_start_timerсвязанный сtimerпараметр.
Измерение времени выполнения нескольких последующих вызовов к тому же ядру (рам) обычно улучшает надежность результатов. Поскольку «нагревание» устройства также улучшает непротиворечивость сравнительного тестирования результатов, рекомендуется вызвать код, ставящий в очередь ядро, по крайней мере, однажды, Вы начинаете синхронизировать. Перечисление 14-1 хранит информацию производительности о ядре, которое это ставит в очередь. Заметьте, как индекс цикла запускается в -2 когда индекс был постепенно увеличен к, но таймер запущен 0. :
Выборка перечисления 14-1 сравнительное тестирование цикла на ядре
const int iter = 10; // number of iterations to benchmark |
cl_timer blockTimer; |
for (int it = -2; it < iter; it++) { // Negative values not timed: warm-up |
if (it == 0) { // start timing |
blockTimer = gcl_start_timer(void); |
} |
<code to benchmark> |
} |
clFinish(queue); |
gcl_stop_timer(blockTimer); |
// t = execution time for one iteration (s) |
double t = blockTimer / (double)iter; |
Генерация Вычислить/Доступ к памяти Пиковый Сравнительный тест
Перед оптимизацией кода необходимо оценить, как быстро определенное устройство GPU при доступе к памяти и при выполнении операций с плавающей точкой. Можно использовать два простых ядра для сравнительного тестирования этих возможностей:
Ядро копии
Ядро в Перечислении 14-2 читает большое изображение (результаты, показанные в этой главе, прибывают из обработки 16 мегапикселей (MP) изображение), сохраненный во входном буфере, и копирует изображение в буфер вывода. Выполнение этого кода дает хорошую индикацию относительно самой лучшей скорости доступа к памяти для ожидания из GPU.
Ядро Копии перечисления 14-2
kernel void copy(global const float * in,
global float * out,
int w,int h)
{int x = get_global_id(0); // (x,y) = pixel to process
int y = get_global_id(1); // in this work item
out[x+y*w] = in[x+y*w]; // Load and Store
}
Графики рисунка 14-2 копируют скорость ядра как функцию размера изображения. Выполняя ядро копии на нашем GPU, мы смогли скопировать 13.5 gigapixels в секунду. Это - хорошая индикация относительно максимальной скорости доступа к памяти на этом устройстве.
Производительность ядра Копии рисунка 14-2 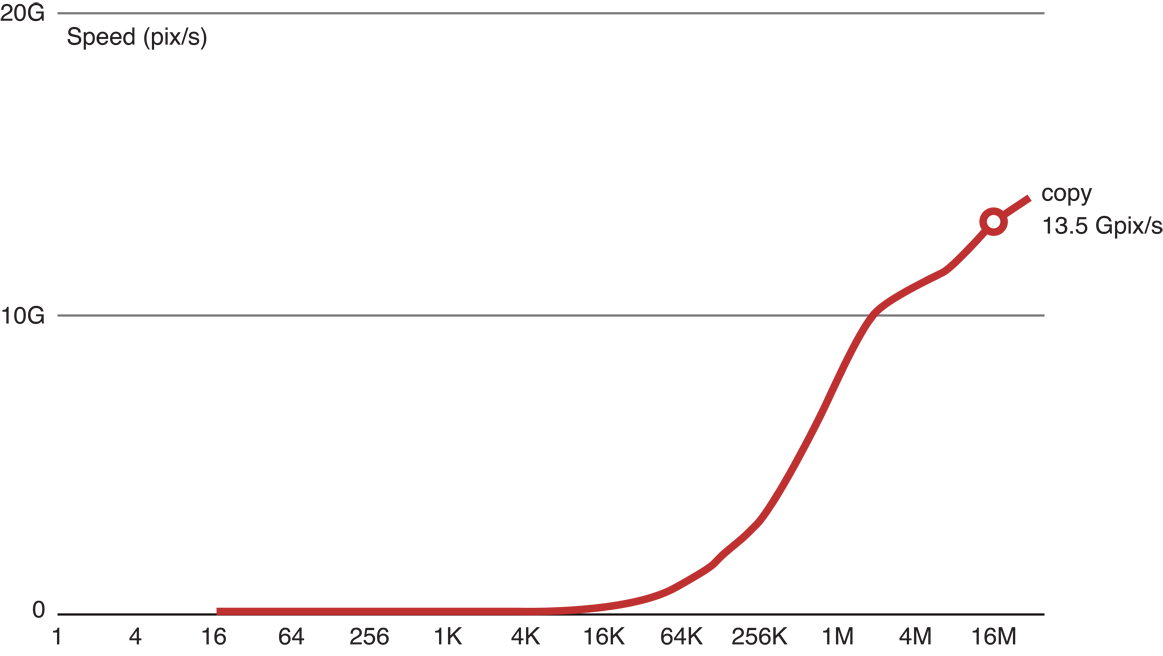
Ядро MAD
В Умножении плюс ADd (MAD) ядро, такое как Перечисление 14-3, большое графическое изображение читается в, некоторые операции с плавающей точкой выполняются на данных изображения, и результаты сохраняются к буферу вывода. Ядро MAD может использоваться для оценки оптимальной скорости обработки GPU, но при использовании ядра MAD, необходимо добавить в достаточном количестве операций с плавающей точкой, чтобы гарантировать, чтобы ограничения памяти не маскировали возможности с плавающей точкой.
Перечисление 14-3 ядро MAD с 3 флопс
kernel void mad3(global const float * in,
global float * out,
int w,int h) {int x = get_global_id(0);
int y = get_global_id(1);
float a = in[x+y*w]; // Load
float b = 3.9f * a * (1.0f-a); // Three floating point ops
out[x+y*w] = b; // Store
}
Сравнительный тест MAD показывает вычислить/память отношение в случае единственной последовательности зависимых операций. Вычислите ядра, может достигнуть, намного выше вычисляют/память отношения, когда они выполняют несколько независимых цепочек зависимости. Например, матрица * матрица умножается, ядро может обработать почти 2 Tflop/s на том же GPU.
Как показано на рисунке 14-3, когда мы добавили три операции с плавающей точкой к коду ядра копии (главная (красная) строка), мы все еще смогли обработать 11,9 GP/с. Это указывает, что только с тремя флопс, обработка остается ограниченной памятью.
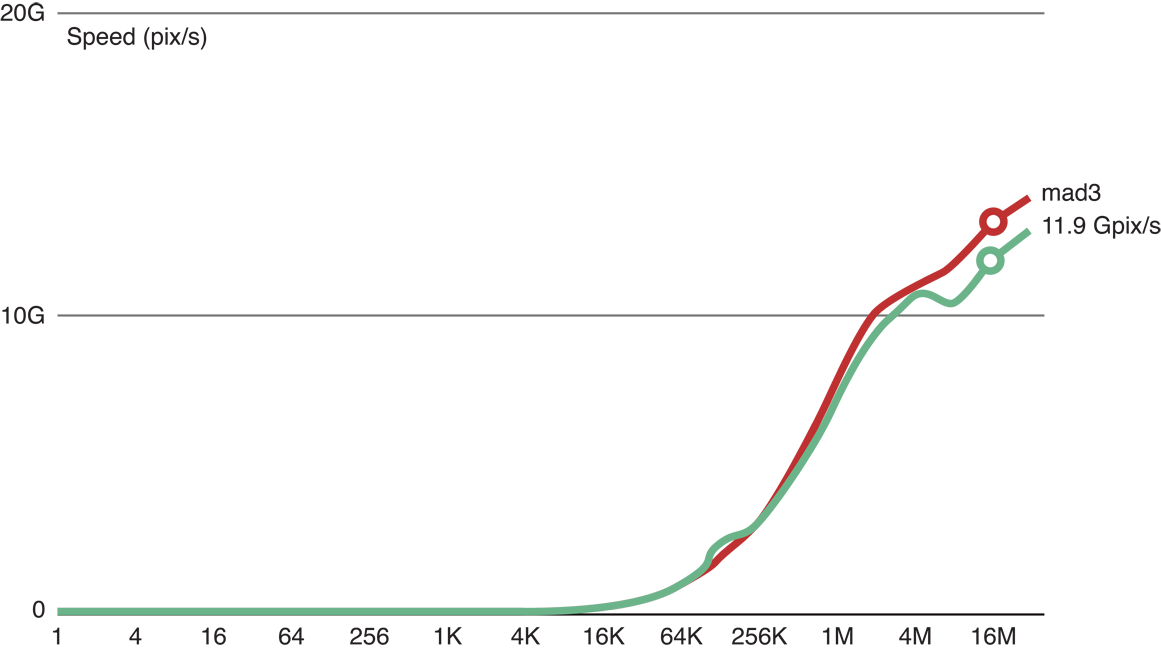
Рисунок 14-4 показывает, что, когда мы добавили шесть операций с плавающей точкой к коду ядра копии (главная (красная) строка), мы все еще в состоянии обработать 11,8 GP/с. Это указывает, что с шестью флопс, обработка все еще ограничена памятью.
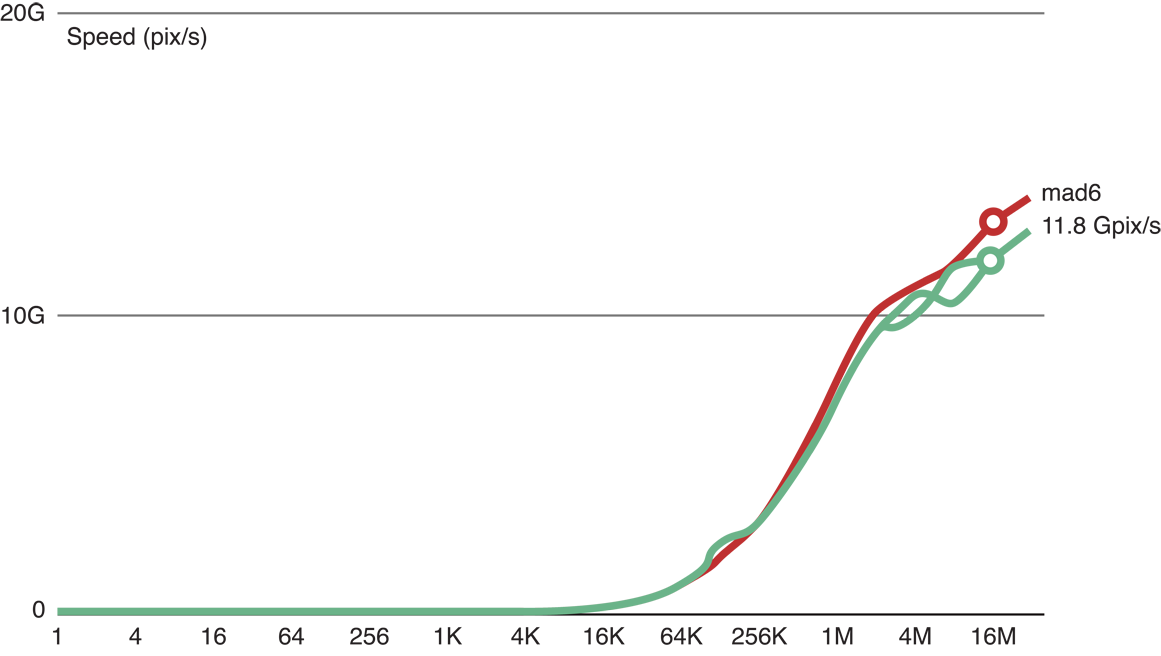
Рисунок 14-5 показывает это после того, как мы добавили 24 операции с плавающей точкой к коду ядра копии (красная строка), обработав замедленный к 10,1 GP/с. Поскольку сокращение скорости обработки является достаточно большим, чтобы считаться значительным, этот результат указывает, что это ядро является хорошим сравнительным тестом для вычислительной обработки для этого GPU.
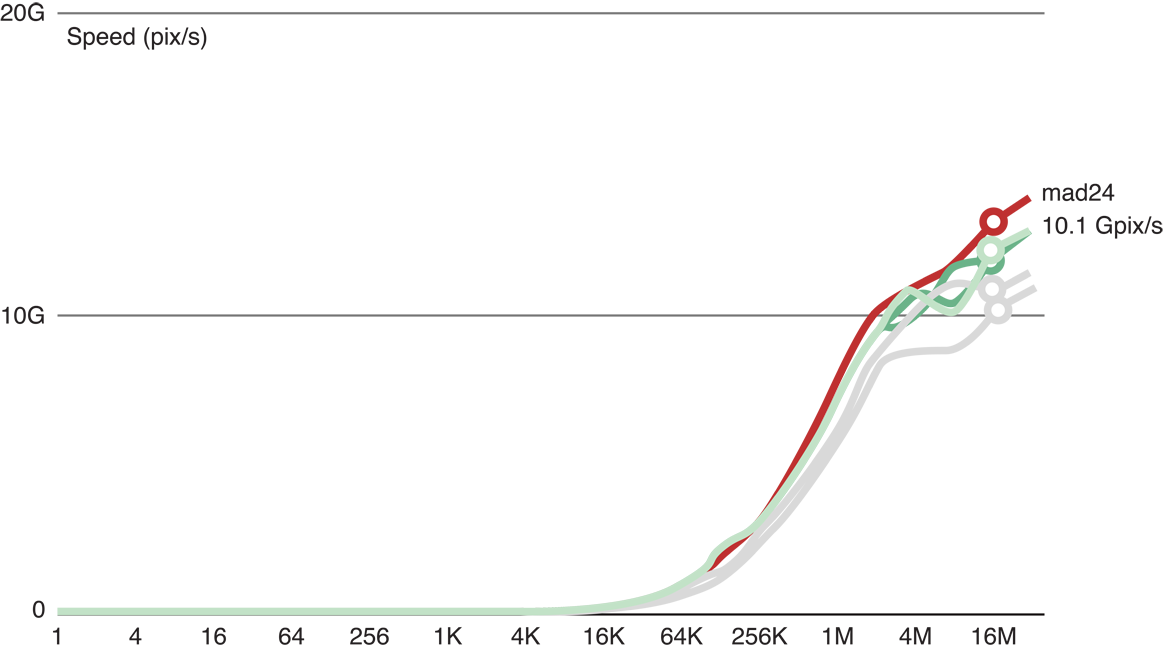
Настройка процедуры
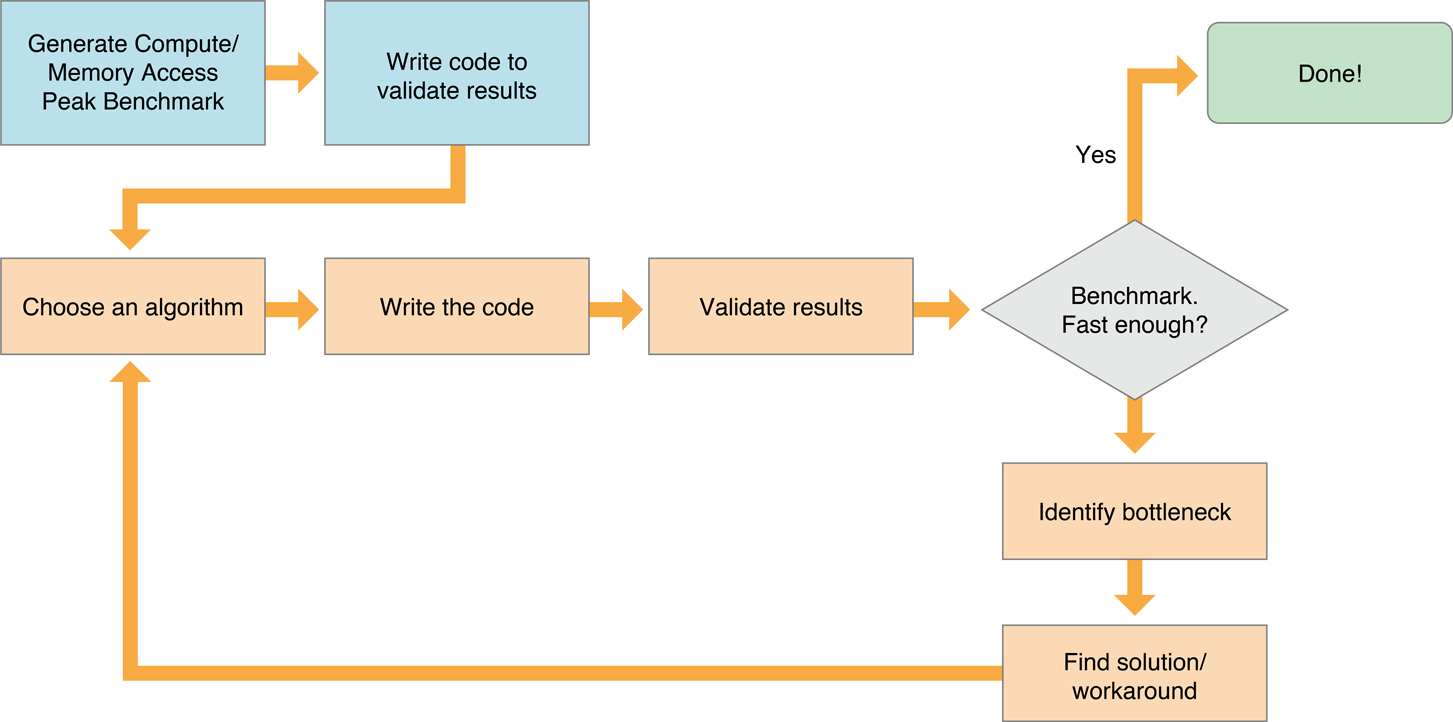
Рисунок 14-6 показывает типичный процесс для оптимизации ядра, работающего эффективно на GPU:

-
Выберите эффективный алгоритм. OpenCL работает наиболее эффективно, если алгоритм оптимизирован для использования в своих интересах возможностей всех устройств, это работает. Посмотрите Выбор Efficient Algorithm для предложений о том, как оценить потенциальные алгоритмы.
-
Запишите код, работающий эффективно на всем целевом устройстве (ах). У каждой семьи GPUs есть уникальная архитектура. Для получения оптимальной производительности от GPU необходимо понять ту архитектуру GPU’s. Например, некоторые семьи GPU выполняют лучше всего, когда блоки доступа к памяти установлены в определенные размеры, другая работа семей GPU лучше всего, когда число элементов в рабочей группе является кратным числом определенного числа и т.д. Консультируйтесь с литературой производителя для любого GPU, который Вы хотите поддерживать для получения подробных данных о той архитектуре GPU’s. Этот документ обеспечивает только общие принципы, которые должны примениться к большей части GPUs.
Посмотрите Таблицу 14-1 для предложений.
Обычно лучше записать, что скаляр кодирует сначала. Во второй итерации параллелизируйте его. Затем, создайте версию, минимизирующую использование памяти.
-
Удостоверьтесь, что проверили результаты, сгенерированные каждой версией кода.
-
Сравнительный тест. Можно использовать методы, описанные в Измерении Производительности На Устройствах для измерения скорости кода сравнительного теста и кода приложения. Если производительность достаточно хороша, Вы сделаны.
-
Идентифицируйте узкие места.
-
Найдите решение или обходное решение.
-
Повторите этот процесс, пока Ваша производительность не приблизится к цели оптимизации.
Выбор эффективного алгоритма
Рассмотрите следующий при выборе алгоритма для приложения OpenCL:
Алгоритм должен быть с массовым параллелизмом, так, чтобы вычисление могло быть выполнено большим количеством независимых единиц работы. Поскольку данные параллельны вычислениям на GPU, работам OpenCL лучше всего, куда много единиц работы представлены устройству.
Минимизируйте использование памяти. GPU имеет огромную вычислительную мощность; ядра обычно ограничены памятью. Следовательно, алгоритмы с наименьшим количеством доступов памяти или алгоритмов с верхним уровнем вычисляют к памяти отношение, являются обычно лучшими для приложений OpenCL. Вычислить к памяти отношение является отношением между числом операций с плавающей точкой и числом байтов, переданных и из памяти.
Попытайтесь максимизировать число независимых цепочек зависимости путем группировки вычисления нескольких выходных элементов в одну единственную единицу работы.
Движущиеся данные к или от устройств OpenCL являются дорогими. OpenCL является самым эффективным на больших наборах данных.
OpenCL дает Вам полный контроль над выделением памяти и передачами памяти устройства хоста. Ваша программа будет работать намного быстрее при выделении памяти на устройстве OpenCL переместите данные в устройство, сделайте как можно больше вычисления на устройстве, затем переместитесь, это прочь — вместо того, чтобы неоднократно пройти через запись вычисляет циклы чтения.
Избегать медленных передач устройства хоста:
Каждый раз, когда возможно, совокупные несколько передач в единственную, большую передачу.
Алгоритмы проекта для хранения данных по устройству максимально долго.
Для параллельных данным вычислений на GPU OpenCL работает лучше всего, где существует много единиц работы, представленных устройству; однако, некоторые алгоритмы намного более эффективны, чем другие.
Используйте OpenCL встроенные функции, когда это возможно. Оптимальный код будет сгенерирован для этих функций.
Точность баланса и скорость. GPUs разработаны для графики, где требования для точности ниже. Самые быстрые варианты представлены в OpenCL, созданном-ins как
fast_,half_,native_функции. Опции сборки программы обеспечивают управление некоторой оптимизации скорости.Выделение и освобождение ресурсы OpenCL (объекты памяти, ядра, и т.д.) занимают время. Снова используйте эти объекты, когда это возможно, вместо того, чтобы выпустить их и неоднократно воссоздать их. Отметьте, однако, что объекты изображения могут быть снова использованы, только если они - тот же размер и формат пикселя по мере необходимости новым изображением.
Используйте в своих интересах подсистему памяти устройства.
При использовании памяти на устройстве OpenCL локальная память, совместно использованная всеми единицами работы в единственной рабочей группе, быстрее, чем глобальная память, совместно использованная всеми рабочими группами на устройстве. Частная память, доступная только единственной единице работы, еще быстрее.
На GPU образец доступа к памяти является наиболее важным фактором. Используйте более быстрые уровни памяти (локальная память, регистры), чтобы противостоять эффектам субоптимального образца и минимизировать доступы к более медленной глобальной памяти.
Экспериментируйте со своим кодом для нахождения размера ядра, работающего лучше всего.
Используя меньшие ядра может быть эффективным, потому что каждое крошечное ядро использует минимальные ресурсы. Разламывание задания на много маленьких ядер допускает создание очень больших, эффективных рабочих групп. С другой стороны, это может потребовать между 10-100 μs для запуска каждого ядра. Когда каждое ядро выходит, результаты должны быть сохранены в глобальной памяти. Поскольку чтение и запись в глобальную память являются дорогими, связывание многих маленьких ядер в одно большое ядро может сохранить значительные издержки.
Для нахождения размера ядра, обеспечивающего оптимальную производительность необходимо будет экспериментировать с кодом.
События OpenCL на GPU являются дорогими.
Можно использовать события для координирования выполнения между очередями, но существуют издержки к выполнению так. Используйте события только там, где это необходимо; иначе используйте в своих интересах чтобы свойства очередей.
Избегите расходящегося выполнения:
Все потоки, запланированные вместе на GPU, должны выполнить тот же код. Как следствие, при выполнении условного выражения, все потоки выполняют оба ответвления, но их вывод отключен, когда они - ложное ответвление. Лучше избегать условных выражений (замените их
a?x:yоператоры), или используют встроенные функции.
Пример: настройка производительности гауссовой размытости
Выполняющие шаги в качестве примера посредством процесса оптимизации приложения, выполняющего Гауссову размытость на изображении на GPU. Можно следовать подобному протоколу при настройке кода GPU.
Оцените оптимальную производительность.
Генерируйте тестовый код. Является, вероятно, самым простым записать ссылочную версию кода узла, сохранить результат, затем записать код для сравнения проверенного вывода с выводом, сгенерированным оптимизированным кодом.
Выберите алгоритм для реализации нашей Гауссовой размытости:
Существует три возможности:
Классическая двумерная свертка
Рисунок 14-7 изображает создание двумерной свертки с помощью 31 x 31 ядро для sigma=5. Это переводит в 31 раз 31 или 961 входной пиксель для каждого пиксельного вывода. Одно дополнение и одно умножение используются для каждого ввода для в общей сложности 961+1 I/O или 2 раза 961 флопс за пиксель. Эти результаты показаны во второй строке Таблицы 14-1.
Классика рисунка 14-7 двумерная свертка 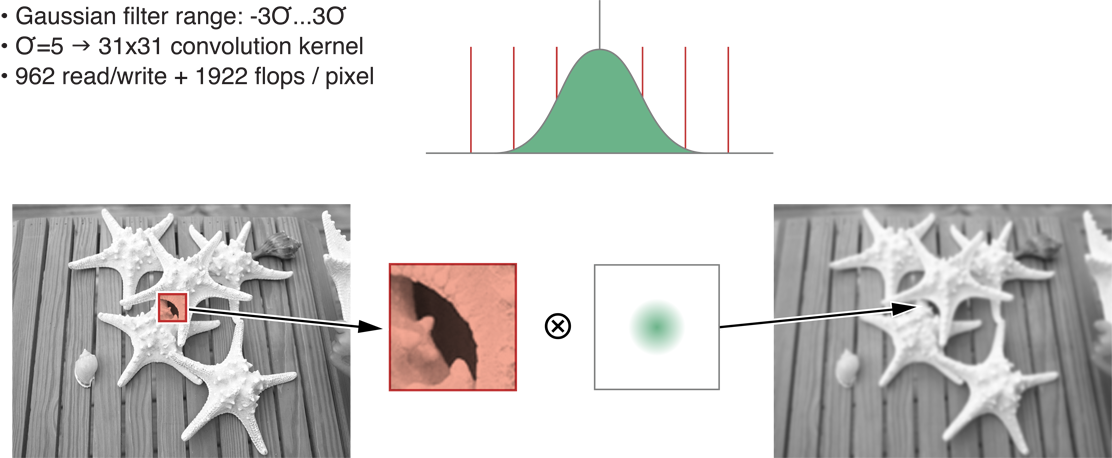
Отделимая двумерная свертка
В этом случае алгоритм отделим. Это может быть разделено на два одномерных фильтра одна горизонталь и одна вертикальная, как показано на рисунке 14-8. Путем разделения размерностей Вы сокращаете стоимость в памяти, и обработка снижается до 64 операций чтения-записи и 124 флопс за пиксель. Эти результаты показаны в третьей строке Таблицы 14-1.
1D свертка с ядром размера 31, который требует чтения 31 входного значения для каждого выходного пикселя, затем выполняя 1 дополнение и 1 умножение для каждого ввода. Этому 31 год + 1 I/O и 2 раза 31 = 62 флопс. Удвойте это для получения чисел для двух передач. (Это является определенным для sigma=5.)
Рисунок 14-8 Отделимая двумерная свертка 

Рекурсивный гауссов фильтр
Этот алгоритм не вычисляет точную Гауссову размытость, только хорошее приближение ее. Как показано на рисунке 14-9, это требует четырех передач (две горизонтали, два вертикальных), но сокращает обработку до 10 операций чтения-записи и 64 флопс за пиксель. Эти результаты показаны в четвертой строке Таблицы 14-1.
Рисунок 14-9 Рекурсивные Гауссовы передачи фильтра 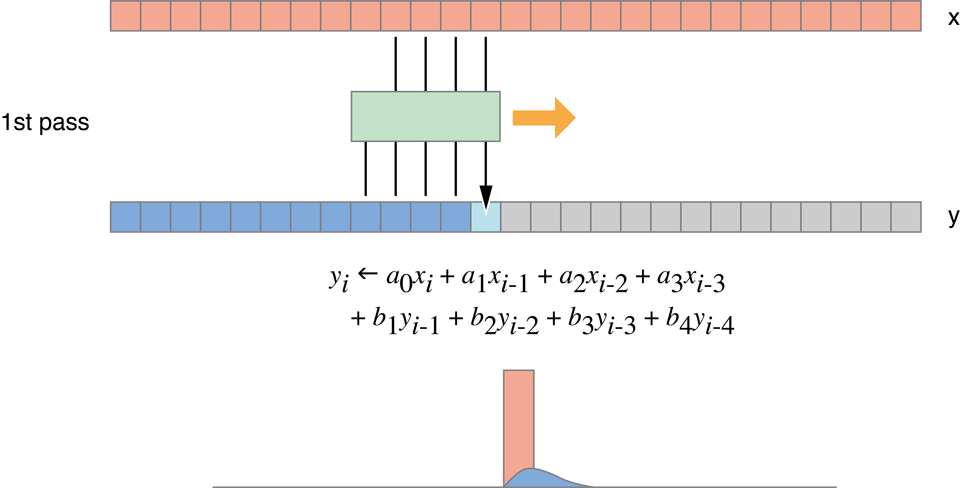
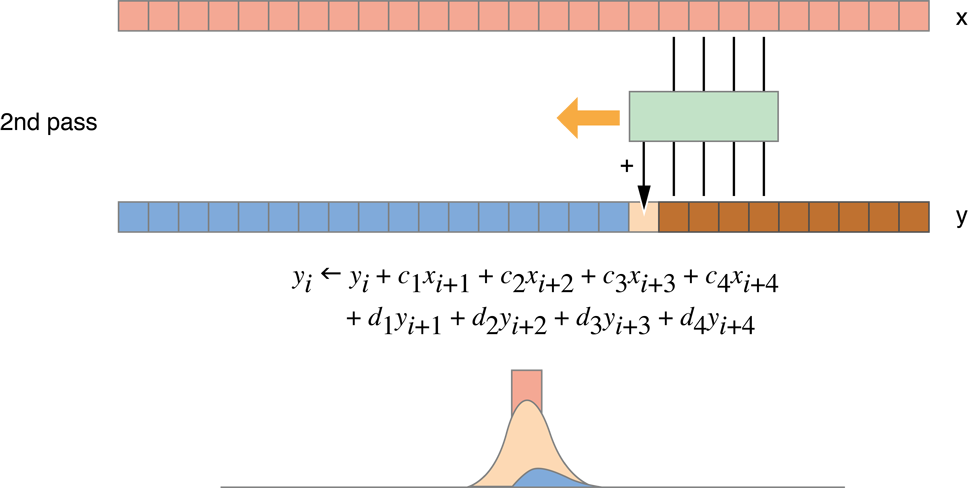
Рисунок 14-10 Рекурсивный Гауссов фильтр 
Таблица 14-1 сравнивает вычислить к памяти результаты отношения 2D Свертки, Отделимой Свертки и Рекурсивных Гауссовых итераций. (Верхний ряд показывает результаты простой копии.) Похоже, что Рекурсивный Гауссов алгоритм выполняет лучше всего:
Табличные 14-1 алгоритмы Сравнения Алгоритм
Память
(пустите в ход R+W),
Вычислить
(флопс)
C/M
Отношение
Оценка
(MP/s)
Копия
2
0
0
14,200
2D Свертка
962
1,922
2
30
Отделимая свертка
64
124
2
443
Рекурсивный гауссов
10
64
6
2,840
Первый столбец изображает число доступов памяти на пиксель. Второй столбец изображает число флопс на пиксель. Третий столбец изображает compute:memory отношение. Последний столбец показывает число мегапикселей, которые каждый алгоритм, как могут ожидать, обработает в секунду; числа были получены путем взятия отношения I/O относительно ядра копии. Ядро копии обрабатывает 14 200 MP/с с 2 I/O на пиксель. Ядро с 64 I/O на пиксель будет в 32 раза медленнее, таким образом, это обработает 14200/32 = 443 MP/с.
Первая версия кода, выполняющего Гауссову размытость с помощью рекурсивного Гауссова алгоритма, похожа на Перечисление 14-4.
Перечисление 14-4 Рекурсивная Гауссова реализация, версия 1
// This is the horizontal pass.
// One work item per output row
// Run one of these functions for each row of the image
// (identified by variable y).
kernel void rgH(global const float * in,global float * out,int w,int h)
{int y = get_global_id(0); // Row to process
// Forward pass
float i1,i2,i3,o1,o2,o3,o4;
i1 = i2 = i3 = o1 = o2 = o3 = o4 = 0.0f;
// In each iteration of the loop, read one input value and
// store one output value.
for (int x=0;x<w;x++)
{float i0 = in[x+y*w]; // Load
float o0 = a0*i0 + a1*i1 + a2*i2 + a3*i3
- c1*o1 - c2*o2 - c3*o3 - c4*o4; // Compute new output
out[x+y*w] = o0; // Store
// Rotate values for next pixel.
i3 = i2; i2 = i1; i1 = i0;
o4 = o3; o3 = o2; o2 = o1; o1 = o0;
}
// Backward pass
...
}
// This is the vertical pass.
// One work item per output column
// Run one of these functions for each column of the image
// (identified by variable x).
kernel void rgV(global const float * in,global float * out,int w,int h)
{int x = get_global_id(0); // Column to process
// Forward pass
float i1,i2,i3,o1,o2,o3,o4;
i1 = i2 = i3 = o1 = o2 = o3 = o4 = 0.0f;
for (int y=0;y<h;y++)
{float i0 = in[x+y*w]; // Load
float o0 = a0*i0 + a1*i1 + a2*i2 + a3*i3
- c1*o1 - c2*o2 - c3*o3 - c4*o4;
out[x+y*w] = o0; // Store
// Rotate values for next pixel
i3 = i2; i2 = i1; i1 = i0;
o4 = o3; o3 = o2; o2 = o1; o1 = o0;
}
// Backward pass
...
}
Эта итерация приводит к результатам как показанные на рисунке 14-11.
Сравнительный тест рисунка 14-11 Рекурсивной Гауссовой реализации, версии 1 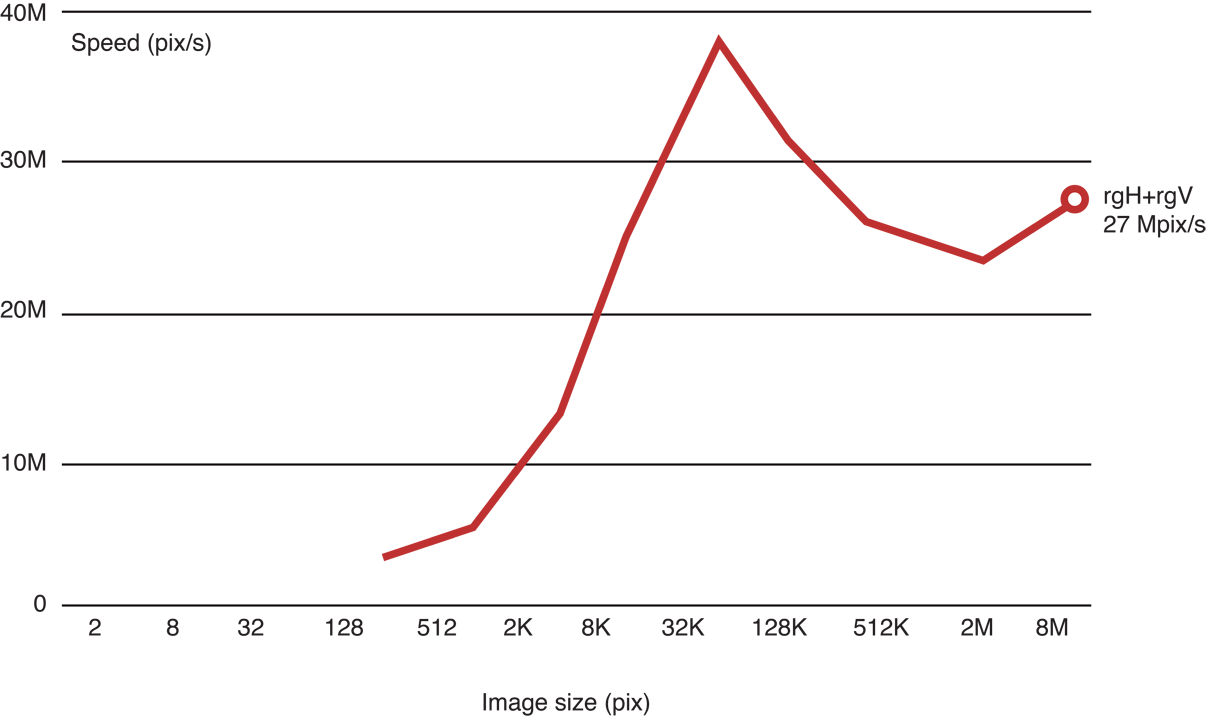
Вертикальная передача быстра, но горизонтальная передача не:
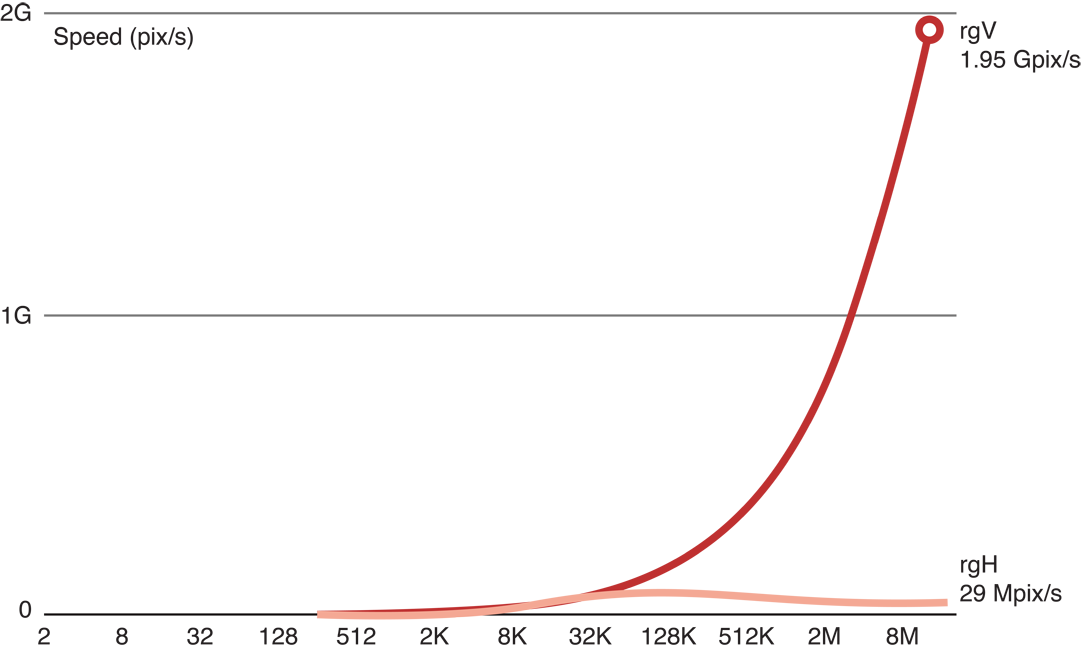
Проблема состоит в том, что в GPU мы запланировали приблизительно 16 миллионов функций, которые вызовут в группах приблизительно из 300 единиц работы одновременно, каждый, одновременно запрашивая доступ к памяти с различным адресом. Это - пример образца доступа к памяти. Аппаратные средства GPU оптимизированы для определенных видов доступов памяти. Другие виды доступов конфликтуют. Они будут сериализированы и будут работать намного медленнее.
В частности, в обработке изображений, когда последовательный доступ единиц работы последовательные пиксели в той же строке, как на рисунке 14-12, обработка очень быстра:
Рисунок 14-12 Последовательные единицы работы, получающие доступ к последовательным адресам 
Однако в случаях, где доступы памяти заканчиваются в том же банке, как на рисунке 14-13 (в обработке изображений это - то, где последовательный доступ единиц работы последовательные пиксели в том же столбце) обработка является медленной:
Рисунок 14-13 , Где доступы памяти заканчиваются в том же банке, обработка, является медленным 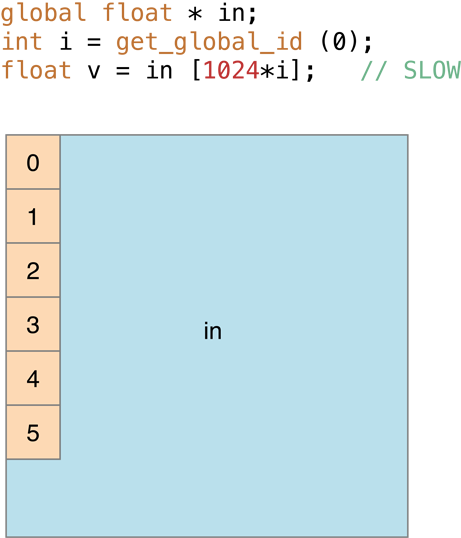
Решение состоит в том, чтобы переместить массив так, чтобы то, что было горизонталью, стало вертикальным. Мы можем обработать перемещенное изображение, затем переместить результат назад в надлежащую ориентацию:
rgV + transpose + rgV + transpose = rgV + rgHДля перемещения мы копируем перемещаемые пиксели:
Рисунок 14-14 A перемещает, действительно копия 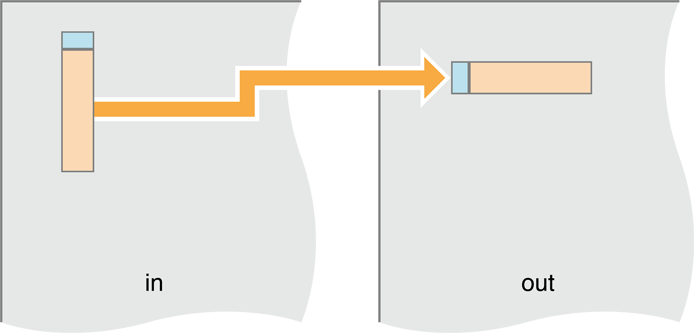
Перемещение должно быть почти с такой скоростью, как ядро копии. Однако несмотря на то, что доступ к входному буферу быстр, доступ к буферу вывода медленнее:

Мы оцениваем производительность перемещать ядра путем добавления двух операций I/O для перемещения для каждой передачи. Это доходит до 10 + 2 * 2 = 14.
Таблица 14-2 Предполагаемые результаты перемещает ядро Алгоритм
Память
(пустите в ход R+W),
Вычислить
(флопс)
C/M
Отношение
Оценка
(MP/s)
V+T+V+T
14
64
4.6
2,030
Когда мы выполняем код, мы видим, что, поскольку высота изображения становится больше, обработка становится медленнее:
Результаты рисунка 14-15 сравнительного тестирования перемещать ядра 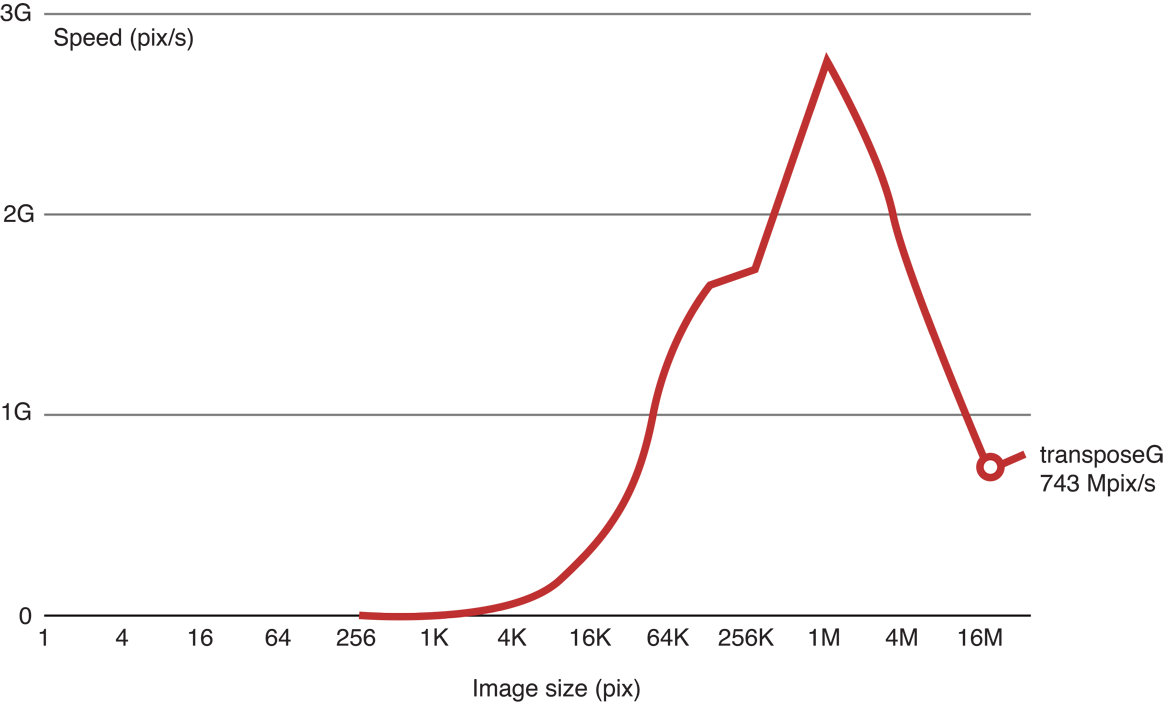
Для ускорения этого мы можем переместить обработку в более быструю память. В GPU обрабатывают ядра (вершина окружает рисунок 14-16). Каждое ядро обработки GPU имеет Арифметико-логические устройства (ALUs), регистры и локальную память. Ядро обработки подключено к глобальной памяти. Глобальная память подключена к узлу. Каждый уровень памяти приблизительно в десять раз быстрее, чем та ниже его.
Рисунок 14-16 иерархия памяти GPU 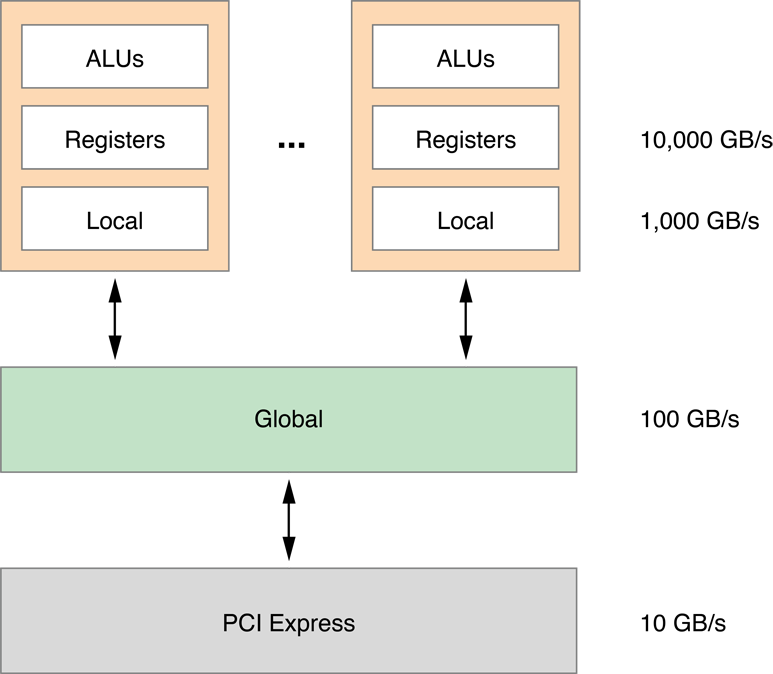
В этой итерации мы переместим обработку в локальную память. У нас будет рабочая группа — блок единиц работы — загрузка маленького блока изображения, храня его в локальной памяти, тогда когда все единицы работы в группе будут закончены, выполняя Гауссову рекурсию на пикселях в локальной памяти, мы выгоняем всех их с квартиры к буферу вывода.
Рисунок 14-17 Движущиеся блоки изображения к локальной памяти 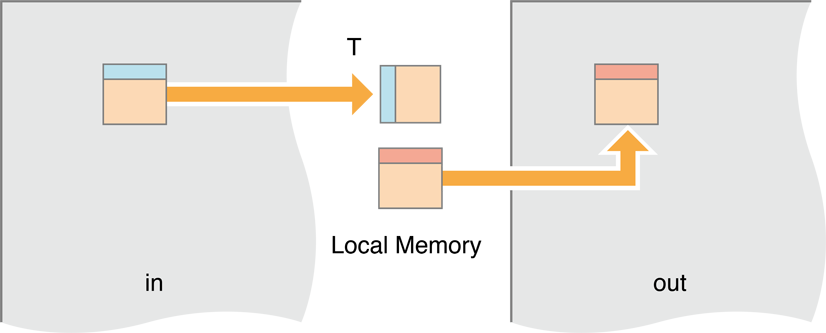
Код, чтобы сделать это похоже на Перечисление 14-5:
Перемещение перечисления 14-5 единицы работы к локальной памяти тогда перемещает
kernel void transposeL(global const float * in,
global float * out,
int w,int h)
{local float aux[256]; // Block size is 16x16
// bx and by are the workgroup coordinates.
// They are mapped to bx and by blocks in the image.
int bx = get_group_id(0), // (bx,by) = input block
by = get_group_id(1);
// ix and iy are the pixel coordinates inside the block.
int ix = get_local_id(0), // (ix,iy) = pixel in block
iy = get_local_id(1);
in += (bx*16)+(by*16)*w; // Move to origin of in,out blocks
out += (by*16)+(bx*16)*h;
// Each work item loads one value to the temporary local memory,
aux[iy+ix*16] = in[ix+w*iy]; // Read block
// Wait for all work items.
// This barrier is needed to make sure all work items in the workgroup
// have executed the aux[…] = in[…] instruction, and that all values
// in aux are correct. Then we can proceed with the out[…] = aux[…].
// This is needed because each work item will set one value of aux
// and then read another one, which was set by another item.
// If we don’t synchronize at this point, we may read an aux value that
// has not yet been set.
barrier(CLK_LOCAL_MEM_FENCE); // Synchronize
// Move the value from the local memory back out to global memory.
// Because copying to consecutive memory, the writes are fast.
out[ix+h*iy] = aux[ix+iy*16]; // Write block
}
К сожалению, это изменение не заставляло код работать быстрее.
Результаты рисунка 14-18 перемещения работы к локальной памяти и затем перемещения. 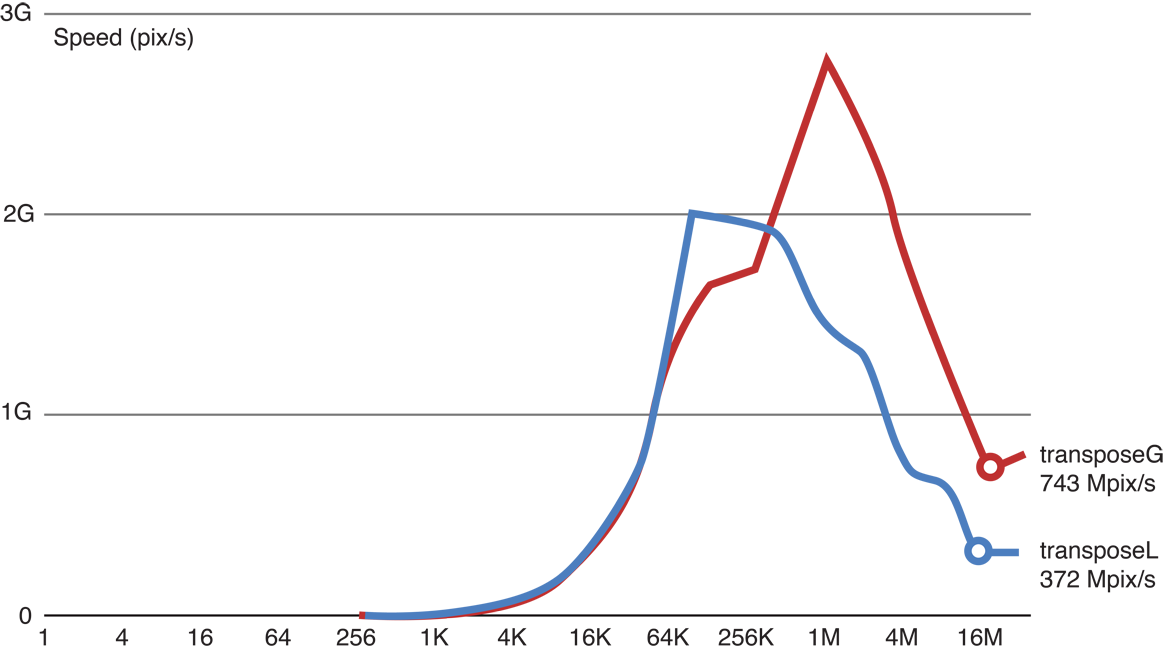
Проблема состоит в том, что теперь мы создали другой образец доступа к памяти, когда мы копируем результаты строк в локальной памяти к столбцам в выводе (глобальная переменная) память.
Образец Доступа к памяти рисунка 14-19 теперь происходит на выходной стороне 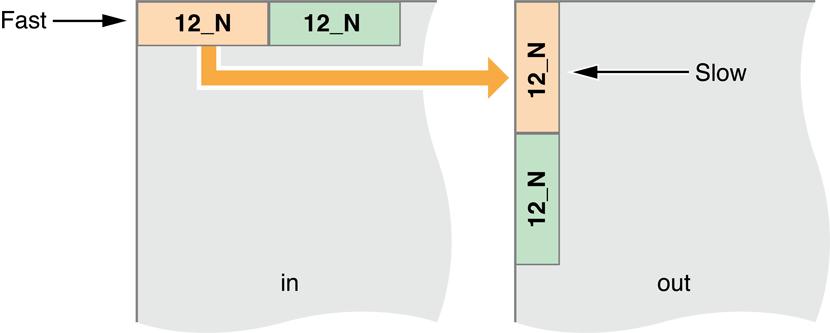
Для решения этого измените рабочие группы на пиксели карты для копирования по диагонали:
Отображение блока Skew рисунка 14-20 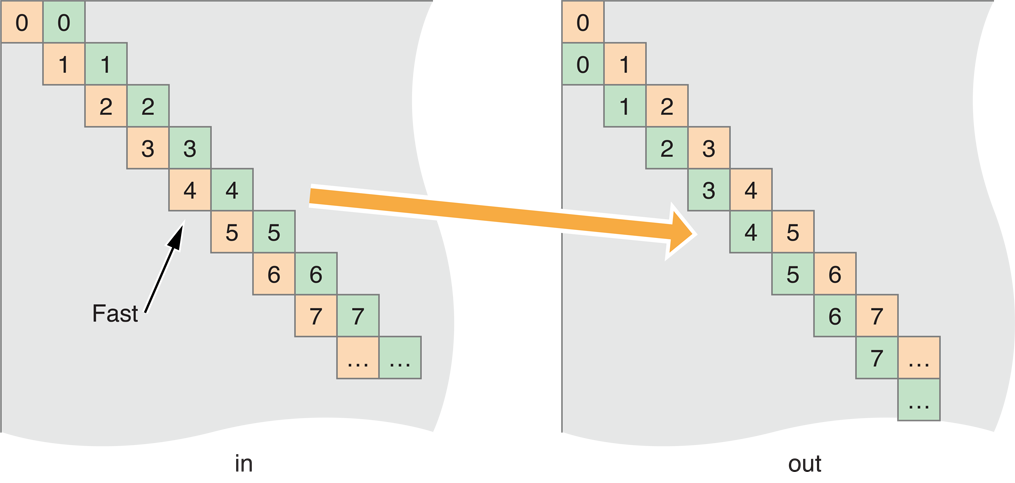
Для преобразования кода для скоса копии ввода и вывода просто измените одну строку:
Изменение перечисления 14-6 код для перемещения по диагонали через изображение
kernel void transposeLS(global const float * in,
global float * out,
int w,int h)
{local float aux[256]; // Block size is 16x16
int bx = get_group_id(0), // (bx,by) = input block
by = get_group_id(1);
int ix = get_local_id(0), // (ix,iy) = pixel in block
iy = get_local_id(1);
// This is the line we changed:
by = (by+bx)%get_num_groups(1); // Skew mapping
in += (bx*16)+(by*16)*w; // Move to origin of in,out blocks
out += (by*16)+(bx*16)*h;
aux[iy+ix*16] = in[ix+w*iy]; // Read block
barrier(CLK_LOCAL_MEM_FENCE); // Synchronize
out[ix+h*iy] = aux[ix+iy*16]; // Write block
}
Сравнительное тестирование доказывает, что эта версия быстрее:
Сравнительный тест рисунка 14-21 скошенного кода 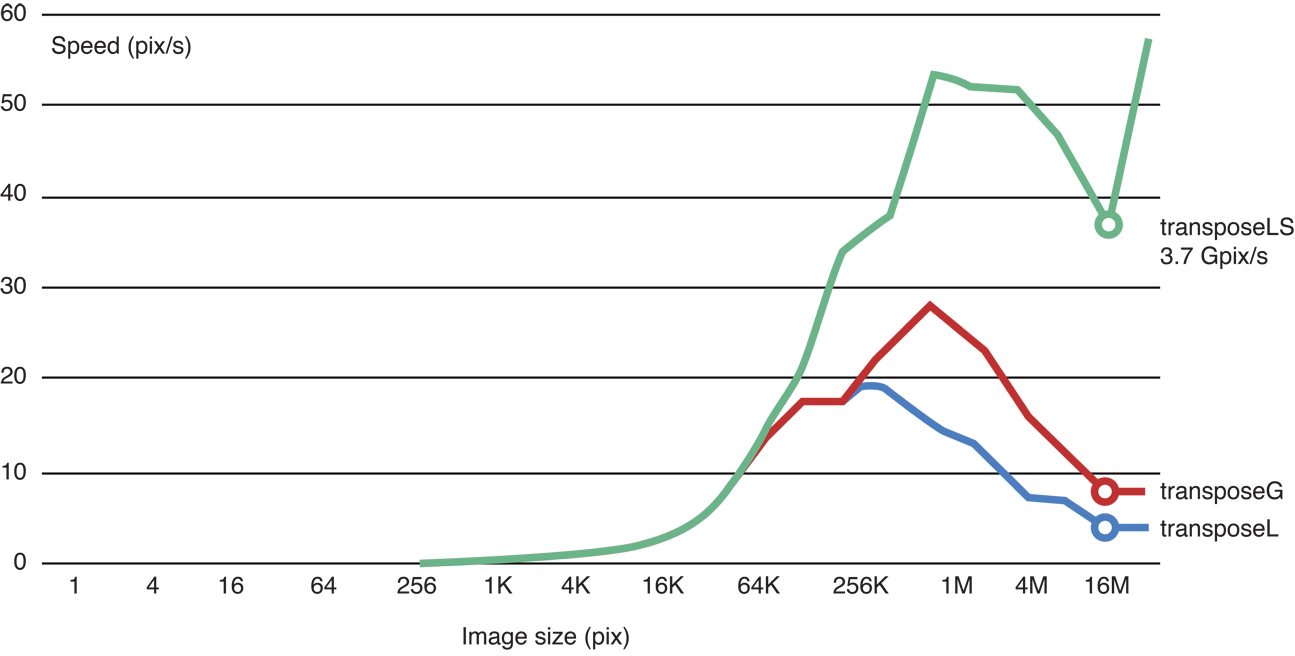
Выполнение перемещенного кода в локальной памяти действительно делает Гауссову размытость значительно быстрее:
Сравнительный тест рисунка 14-22 перемещенного, скошенного кода 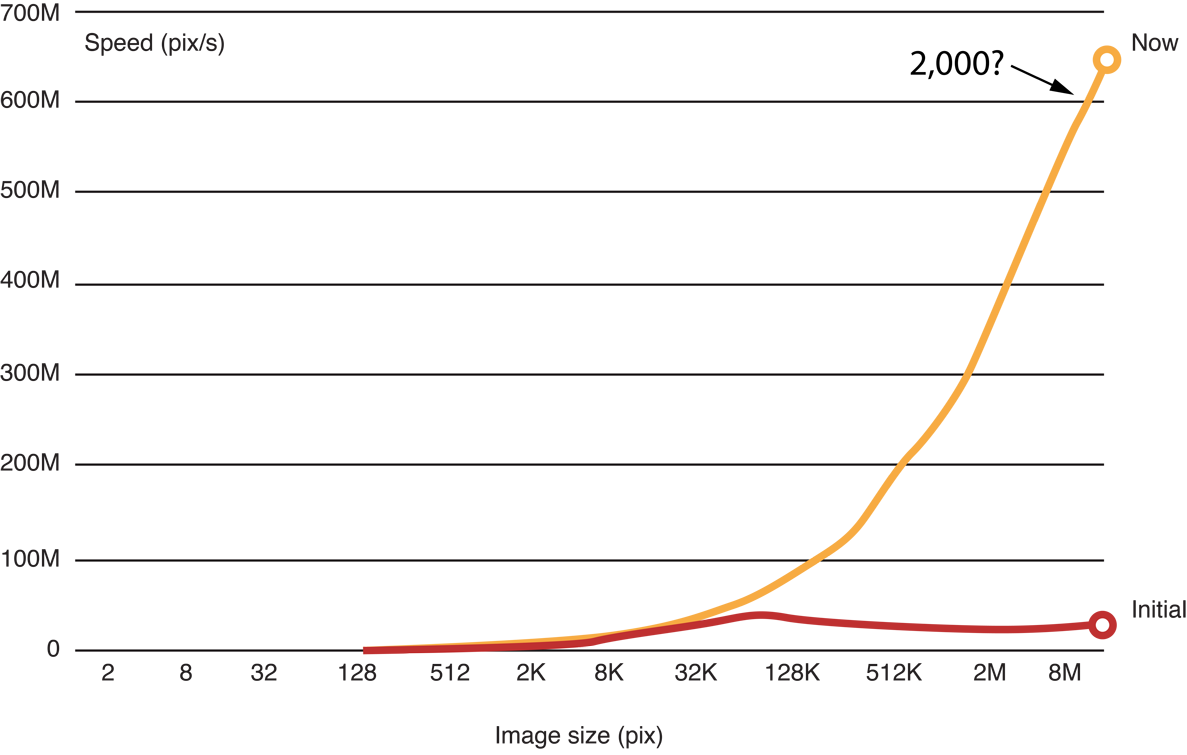
Однако, обработка не происходит так быстро, как наша исходная оценка скорости указала бы. Проблема состоит в том, что из-за последовательной природы рекурсивного Гауссова цикла, у нас нет достаточного количества рабочих групп для насыщения GPU. Мы должны были бы изменить алгоритм для увеличения уровня параллелизма для увеличения производительности для встречи нашей первоначальной оценки.
Инструкции для сокращения наверху на GPU
Некоторые общие принципы для того, чтобы повысить эффективность Вашего кода OpenCL, работающего на GPU:
Создание программы OpenCL является в вычислительном отношении дорогим и должно идеально произойти только один раз в процессе.
Обязательно используйте в своих интересах инструменты в OS X v10.7 или позже которые позволяют Вам компилировать один раз и затем работать много раз. Если Вы действительно примете решение скомпилировать ядро в течение времени выполнения, то необходимо будет выполнить то ядро много раз для амортизации стоимости компиляции его. Можно сохранить двоичный файл после первого раза, когда программа выполняется, и снова используйте скомпилированный код на последующих вызовах, но быть подготовленным перекомпилировать ядро, если сборка перестала работать из-за версии OpenCL или изменения в аппаратных средствах хост-машины.
Можно также использовать bitcode, сгенерированный компилятором OpenCL вместо исходного кода. Используя скомпилированный bitcode увеличит скорость обработки и улучшает потребность в Вас поставить исходный код с Вашим приложением.
Используйте OpenCL встроенные функции, когда это возможно. Оптимальный код будет сгенерирован для этих функций.
Точность баланса и скорость. GPUs разработаны для графики, где требования для точности ниже. Самые быстрые варианты представлены в OpenCL, созданном-ins как
fast_,half_,native_функции. Опции сборки программы позволяют управление некоторой оптимизации скорости.Избегите расходящегося выполнения. На GPU все потоки, запланированные вместе, должны выполнить тот же код. Как следствие, при выполнении условного выражения, все потоки выполняют оба ответвления с их выводом, отключенным, когда они находятся в неправильном ответвлении. Лучше избегать условных выражений (замените их
a?x:yоператоры), или используют встроенные функции.Попытайтесь использовать объекты изображения вместо буферов. В некоторых случаях (для определенных образцов доступа к памяти), различный аппаратный канал передачи данных использование GPU при доступе к изображениям может быть быстрее чем при использовании буферов. Используя изображения, а не буферы особенно важно, когда Вы используете 16-разрядные данные с плавающей точкой (
half).
