

|
Spec-Zone .ru
спецификации, руководства, описания, API
|
| Contents | Prev | Next | Index | Java Language Specification Third Edition |
CHAPTER 15
Much of the work in a program is done by evaluating expressions, either for their side effects, such as assignments to variables, or for their values, which can be used as arguments or operands in larger expressions, or to affect the execution sequence in statements, or both.
This chapter specifies the meanings of expressions and the rules for their evaluation.
An expression denotes nothing if and only if it is a method invocation (§15.12) that invokes a method that does not return a value, that is, a method declared void (§8.4). Such an expression can be used only as an expression statement (§14.8), because every other context in which an expression can appear requires the expression to denote something. An expression statement that is a method invocation may also invoke a method that produces a result; in this case the value returned by the method is quietly discarded.
Value set conversion (§5.1.13) is applied to the result of every expression that produces a value.
Each expression occurs in either:
If the value of a variable of type float or double is used in this manner, then value set conversion (§5.1.13) is applied to the value of the variable.
The value of an expression is assignment compatible (§5.2) with the type of the expression, unless heap pollution (§4.12.2.1) occurs. Likewise the value stored in a variable is always compatible with the type of the variable, unless heap pollution occurs. In other words, the value of an expression whose type is T is always suitable for assignment to a variable of type T.
Note that an expression whose type is a class type F that is declared final is guaranteed to have a value that is either a null reference or an object whose class is F itself, because final types have no subclasses.
float or double, then there is a question as to what value set (§4.2.3) the value of the expression is drawn from. This is governed by the rules of value set conversion (§5.1.13); these rules in turn depend on whether or not the expression is FP-strict.
Every compile-time constant expression (§15.28) is FP-strict. If an expression is not a compile-time constant expression, then consider all the class declarations, interface declarations, and method declarations that contain the expression. If any such declaration bears the strictfp modifier, then the expression is FP-strict.
If a class, interface, or method, X, is declared strictfp, then X and any class, interface, method, constructor, instance initializer, static initializer or variable initializer within X is said to be FP-strict. Note that an annotation (§9.7) element value (§9.6) is always FP-strict, because it is always a compile-time constant (§15.28).
It follows that an expression is not FP-strict if and only if it is not a compile-time constant expression and it does not appear within any declaration that has the strictfp modifier.
Within an FP-strict expression, all intermediate values must be elements of the float value set or the double value set, implying that the results of all FP-strict expressions must be those predicted by IEEE 754 arithmetic on operands represented using single and double formats. Within an expression that is not FP-strict, some leeway is granted for an implementation to use an extended exponent range to represent intermediate results; the net effect, roughly speaking, is that a calculation might produce "the correct answer" in situations where exclusive use of the float value set or double value set might result in overflow or underflow.
null, is not necessarily known at compile time. There are a few places in the Java programming language where the actual class of a referenced object affects program execution in a manner that cannot be deduced from the type of the expression. They are as follows:
o.m(...) is chosen based on the methods that are part of the class or interface that is the type of o. For instance methods, the class of the object referenced by the run-time value of o participates because a subclass may override a specific method already declared in a parent class so that this overriding method is invoked. (The overriding method may or may not choose to further invoke the original overridden m method.)
instanceof operator (§15.20.2). An expression whose type is a reference type may be tested using instanceof to find out whether the class of the object referenced by the run-time value of the expression is assignment compatible (§5.2) with some other reference type.
[] to be treated as a subtype of T[] if S is a subtype of T, but this requires a run-time check for assignment to an array component, similar to the check performed for a cast.
catch clause only if the class of the thrown exception object is an instanceof the type of the formal parameter of the catch clause.
In addition, there are situations where the statically known type may not be accurate at run-time. Such situations can arise in a program that gives rise to unchecked warnings. Such warnings are given in response to operations that cannot be statically guaranteed to be safe, and cannot immediately be subjected to dynamic checking because they involve non-reifiable (§4.7) types. As a result, dynamic checks later in the course of program execution may detect inconsistencies and result in run-time type errors.
A run-time type error can occur only in these situations:
ClassCastException is thrown.
ArrayStoreException is thrown.
catch handler (§11.3); in this case the thread of control that encountered the exception first invokes the method uncaughtException for its thread group and then terminates.
If, however, evaluation of an expression throws an exception, then the expression is said to complete abruptly. An abrupt completion always has an associated reason, which is always a throw with a given value.
Run-time exceptions are thrown by the predefined operators as follows:
OutOfMemoryError if there is insufficient memory available.
NegativeArraySizeException if the value of any dimension expression is less than zero (§15.10).
NullPointerException if the value of the object reference expression is null.
NullPointerException if the target reference is null.
NullPointerException if the value of the array reference expression is null.
ArrayIndexOutOfBoundsException if the value of the array index expression is negative or greater than or equal to the length of the array.
ClassCastException if a cast is found to be impermissible at run time.
ArithmeticException if the value of the right-hand operand expression is zero.
OutOfMemoryError as a result of boxing conversion (§5.1.7).
ArrayStoreException when the value to be assigned is not compatible with the component type of the array.
If an exception occurs, then evaluation of one or more expressions may be terminated before all steps of their normal mode of evaluation are complete; such expressions are said to complete abruptly. The terms "complete normally" and "complete abruptly" are also applied to the execution of statements (§14.1). A statement may complete abruptly for a variety of reasons, not just because an exception is thrown.
If evaluation of an expression requires evaluation of a subexpression, abrupt completion of the subexpression always causes the immediate abrupt completion of the expression itself, with the same reason, and all succeeding steps in the normal mode of evaluation are not performed.
It is recommended that code not rely crucially on this specification. Code is usually clearer when each expression contains at most one side effect, as its outermost operation, and when code does not depend on exactly which exception arises as a consequence of the left-to-right evaluation of expressions.
Thus:
class Test {
public static void main(String[] args) {
int i = 2;
int j = (i=3) * i;
System.out.println(j);
}
}
It is not permitted for it to print9
6 instead of 9.If the operator is a compound-assignment operator (§15.26.2), then evaluation of the left-hand operand includes both remembering the variable that the left-hand operand denotes and fetching and saving that variable's value for use in the implied combining operation. So, for example, the test program:
class Test {
public static void main(String[] args) {
int a = 9;
a += (a = 3); // first example
System.out.println(a);
int b = 9;
b = b + (b = 3); // second example
System.out.println(b);
}
}
because the two assignment statements both fetch and remember the value of the left-hand operand, which is12 12
9, before the right-hand operand of the addition is evaluated, thereby setting the variable to 3. It is not permitted for either example to produce the result 6. Note that both of these examples have unspecified behavior in C, according to the ANSI/ISO standard.If evaluation of the left-hand operand of a binary operator completes abruptly, no part of the right-hand operand appears to have been evaluated.
Thus, the test program:
class Test {
public static void main(String[] args) {
int j = 1;
try {
int i = forgetIt() / (j = 2);
} catch (Exception e) {
System.out.println(e);
System.out.println("Now j = " + j);
}
}
static int forgetIt() throws Exception {
throw new Exception("I'm outta here!");
}
}
That is, the left-hand operandjava.lang.Exception: I'm outta here! Now j = 1
forgetIt() of the operator / throws an exception before the right-hand operand is evaluated and its embedded assignment of 2 to j occurs.&&, ||, and ? :) appears to be fully evaluated before any part of the operation itself is performed.
If the binary operator is an integer division / (§15.17.2) or integer remainder % (§15.17.3), then its execution may raise an ArithmeticException, but this exception is thrown only after both operands of the binary operator have been evaluated and only if these evaluations completed normally.
So, for example, the program:
class Test {
public static void main(String[] args) {
int divisor = 0;
try {
int i = 1 / (divisor * loseBig());
} catch (Exception e) {
System.out.println(e);
}
}
static int loseBig() throws Exception {
throw new Exception("Shuffle off to Buffalo!");
}
}
and not:java.lang.Exception: Shuffle off to Buffalo!
since no part of the division operation, including signaling of a divide-by-zero exception, may appear to occur before the invocation ofjava.lang.ArithmeticException: / by zero
loseBig completes, even though the implementation may be able to detect or infer that the division operation would certainly result in a divide-by-zero exception.
In the case of floating-point calculations, this rule applies also for infinity and not-a-number (NaN) values. For example, !(x<y) may not be rewritten as x>=y, because these expressions have different values if either x or y is NaN or both are NaN.
Specifically, floating-point calculations that appear to be mathematically associative are unlikely to be computationally associative. Such computations must not be naively reordered.
For example, it is not correct for a Java compiler to rewrite 4.0*x*0.5 as 2.0*x; while roundoff happens not to be an issue here, there are large values of x for which the first expression produces infinity (because of overflow) but the second expression produces a finite result.
So, for example, the test program:
strictfp class Test {
public static void main(String[] args) {
double d = 8e+307;
System.out.println(4.0 * d * 0.5);
System.out.println(2.0 * d);
}
}
because the first expression overflows and the second does not.Infinity 1.6e+308
In contrast, integer addition and multiplication are provably associative in the Java programming language.
For example a+b+c, where a, b, and c are local variables (this simplifying assumption avoids issues involving multiple threads and volatile variables), will always produce the same answer whether evaluated as (a+b)+c or a+(b+c); if the expression b+c occurs nearby in the code, a smart compiler may be able to use this common subexpression.
Thus:
class Test {
public static void main(String[] args) {
String s = "going, ";
print3(s, s, s = "gone");
}
static void print3(String a, String b, String c) {
System.out.println(a + b + c);
}
}
because the assignment of the stringgoing, going, gone
"gone" to s occurs after the first two arguments to print3 have been evaluated.If evaluation of an argument expression completes abruptly, no part of any argument expression to its right appears to have been evaluated.
Thus, the example:
class Test {
static int id;
public static void main(String[] args) {
try {
test(id = 1, oops(), id = 3);
} catch (Exception e) {
System.out.println(e + ", id=" + id);
}
}
static int oops() throws Exception {
throw new Exception("oops");
}
static int test(int a, int b, int c) {
return a + b + c;
}
}
because the assignment ofjava.lang.Exception: oops, id=1
3 to id is not executed.
Primary:
PrimaryNoNewArray
ArrayCreationExpression
PrimaryNoNewArray:
Literal
Type . class
void . class
this
ClassName.this
( Expression )
ClassInstanceCreationExpression
FieldAccess
MethodInvocation
ArrayAccess
The following production from §3.10 is repeated here for convenience:
Literal:
IntegerLiteral
FloatingPointLiteral
BooleanLiteral
CharacterLiteral
StringLiteral
NullLiteral
L or l is long; the type of any other integer literal is int.
F or f is float and its value must be an element of the float value set (§4.2.3). The type of any other floating-point literal is double and its value must be an element of the double value set.
boolean.
char.
String.
null is the null type; its value is the null reference.
void, followed by a `.' and the token class. The type of a class literal, C.Class, where C is the name of a class, interface or array type, is Class<C>. If p is the name of a primitive type, let B be the type of an expression of type p after boxing conversion (§5.1.7). Then the type of p.class is Class<B>. The type of void.class is Class<Void>.
A class literal evaluates to the Class object for the named type (or for void) as defined by the defining class loader of the class of the current instance.
It is a compile time error if any of the following occur:
this may be used only in the body of an instance method, instance initializer or constructor, or in the initializer of an instance variable of a class. If it appears anywhere else, a compile-time error occurs.
When used as a primary expression, the keyword this denotes a value that is a reference to the object for which the instance method was invoked (§15.12), or to the object being constructed. The type of this is the class C within which the keyword this occurs. At run time, the class of the actual object referred to may be the class C or any subclass of C.
In the example:
class IntVector {
int[] v;
boolean equals(IntVector other) {
if (this == other)
return true;
if (v.length != other.v.length)
return false;
for (int i = 0; i < v.length; i++)
if (v[i] != other.v[i])
return false;
return true;
}
}
IntVector implements a method equals, which compares two vectors. If the other vector is the same vector object as the one for which the equals method was invoked, then the check can skip the length and value comparisons. The equals method implements this check by comparing the reference to the other object to this.
The keyword this is also used in a special explicit constructor invocation statement, which can appear at the beginning of a constructor body (§8.8.7).
Let C be the class denoted by ClassName. Let n be an integer such that C is the nth lexically enclosing class of the class in which the qualified this expression appears. The value of an expression of the form ClassName.this is the nth lexically enclosing instance of this (§8.1.3). The type of the expression is C. It is a compile-time error if the current class is not an inner class of class C or C itself.
The use of parentheses only effects the order of evaluation, with one fascinating exception.
Discussion
Consider the case if the smallest possible negative value of type long. This value, 9223372036854775808L, is allowed only as an operand of the unary minus operator (§3.10.1). Therefore, enclosing it in parentheses, as in -(9223372036854775808L) causes a compile time error.
In particular, the presence or absence of parentheses around an expression does not (except for the case noted above) affect in any way:
float or double.
ClassInstanceCreationExpression:
new TypeArgumentsopt ClassOrInterfaceType ( ArgumentListopt )
ClassBodyopt
Primary. new TypeArgumentsopt Identifier TypeArgumentsopt (
ArgumentListopt ) ClassBodyopt
ArgumentList:
Expression
ArgumentList , Expression
new. An unqualified class instance creation expression may be used to create an instance of a class, regardless of whether the class is a top-level (§7.6), member (§8.5, §9.5), local (§14.3) or anonymous class (§15.9.5).
We say that a class is instantiated when an instance of the class is created by a class instance creation expression. Class instantiation involves determining what class is to be instantiated, what the enclosing instances (if any) of the newly created instance are, what constructor should be invoked to create the new instance and what arguments should be passed to that constructor.
final class. If T denotes an interface then an anonymous direct subclass of Object that implements the interface named by T is declared. In either case, the body of the subclass is the ClassBody given in the class instance creation expression. The class being instantiated is the anonymous subclass.
final inner class (§8.1.3) that is a member of the compile-time type of the Primary. It is also a compile-time error if T is ambiguous (§8.5) or if T denotes an enum type. An anonymous direct subclass of the class named by T is declared. The body of the subclass is the ClassBody given in the class instance creation expression. The class being instantiated is the anonymous subclass.
abstract, or a compile-time error occurs. In this case, the class being instantiated is the class denoted by ClassOrInterfaceType.
abstract inner class (§8.1.3) T that is a member of the compile-time type of the Primary. It is also a compile-time error if Identifier is ambiguous (§8.5), or if Identifier denotes an enum type (§8.9). The class being instantiated is the class denoted by Identifier.
this (§8.1.3).
this.
this.
this.
First, if the class instance creation expression is a qualified class instance creation expression, the qualifying primary expression is evaluated. If the qualifying expression evaluates to null, a NullPointerException is raised, and the class instance creation expression completes abruptly. If the qualifying expression completes abruptly, the class instance creation expression completes abruptly for the same reason.
Next, space is allocated for the new class instance. If there is insufficient space to allocate the object, evaluation of the class instance creation expression completes abruptly by throwing an OutOfMemoryError (§15.9.6).
The new object contains new instances of all the fields declared in the specified class type and all its superclasses. As each new field instance is created, it is initialized to its default value (§4.12.5).
Next, the actual arguments to the constructor are evaluated, left-to-right. If any of the argument evaluations completes abruptly, any argument expressions to its right are not evaluated, and the class instance creation expression completes abruptly for the same reason.
Next, the selected constructor of the specified class type is invoked. This results in invoking at least one constructor for each superclass of the class type. This process can be directed by explicit constructor invocation statements (§8.8) and is described in detail in §12.5.
The value of a class instance creation expression is a reference to the newly created object of the specified class. Every time the expression is evaluated, a fresh object is created.
An anonymous class is never abstract (§8.1.1.1). An anonymous class is always an inner class (§8.1.3); it is never static (§8.1.1, §8.5.2). An anonymous class is always implicitly final (§8.1.1.2).
The body of the constructor consists of an explicit constructor invocation (§8.8.7.1) of the form super(...), where the actual arguments are the formal parameters of the constructor, in the order they were declared.
super(...), where o is the first formal parameter of the constructor, and the actual arguments are the subsequent formal parameters of the constructor, in the order they were declared.
throws clause of an anonymous constructor must list all the checked exceptions thrown by the explicit superclass constructor invocation statement contained within the anonymous constructor, and all checked exceptions thrown by any instance initializers or instance variable initializers of the anonymous class.Note that it is possible for the signature of the anonymous constructor to refer to an inaccessible type (for example, if such a type occurred in the signature of the superclass constructor cs). This does not, in itself, cause any errors at either compile time or run time.
OutOfMemoryError is thrown. This check occurs before any argument expressions are evaluated.So, for example, the test program:
class List {
int value;
List next;
static List head = new List(0);
List(int n) { value = n; next = head; head = this; }
}
class Test {
public static void main(String[] args) {
int id = 0, oldid = 0;
try {
for (;;) {
++id;
new List(oldid = id);
}
} catch (Error e) {
System.out.println(e + ", " + (oldid==id));
}
}
}
because the out-of-memory condition is detected before the argument expressionjava.lang.OutOfMemoryError: List, false
oldid = id is evaluated.Compare this to the treatment of array creation expressions (§15.10), for which the out-of-memory condition is detected after evaluation of the dimension expressions (§15.10.3).
ArrayCreationExpression:
new PrimitiveType DimExprs Dimsopt
new ClassOrInterfaceType DimExprs Dimsopt
new PrimitiveType Dims ArrayInitializer
new ClassOrInterfaceType Dims ArrayInitializer
DimExprs:
DimExpr
DimExprs DimExpr
DimExpr:
[ Expression ]
Dims:
[ ]
Dims [ ]
abstract class type (§8.1.1.1) or an interface type (§9). Discussion
The rules above imply that the element type in an array creation expression cannot be a parameterized type, other than an unbounded wildcard.
The type of the creation expression is an array type that can denoted by a copy of the creation expression from which the new keyword and every DimExpr expression and array initializer have been deleted.
For example, the type of the creation expression:
is:new double[3][3][]
The type of each dimension expression within a DimExpr must be a type that is convertible (§5.1.8) to an integral type, or a compile-time error occurs. Each expression undergoes unary numeric promotion (§). The promoted type must bedouble[][][]
int, or a compile-time error occurs; this means, specifically, that the type of a dimension expression must not be long.If an array initializer is provided, the newly allocated array will be initialized with the values provided by the array initializer as described in §10.6.
First, the dimension expressions are evaluated, left-to-right. If any of the expression evaluations completes abruptly, the expressions to the right of it are not evaluated.
Next, the values of the dimension expressions are checked. If the value of any DimExpr expression is less than zero, then an NegativeArraySizeException is thrown.
Next, space is allocated for the new array. If there is insufficient space to allocate the array, evaluation of the array creation expression completes abruptly by throwing an OutOfMemoryError.
Then, if a single DimExpr appears, a single-dimensional array is created of the specified length, and each component of the array is initialized to its default value (§4.12.5).
If an array creation expression contains N DimExpr expressions, then it effectively executes a set of nested loops of depth N-1 to create the implied arrays of arrays.
For example, the declaration:
is equivalent in behavior to:float[][] matrix = new float[3][3];
float[][] matrix = new float[3][];
for (int d = 0; d < matrix.length; d++)
matrix[d] = new float[3];
is equivalent to:Age[][][][][] Aquarius = new Age[6][10][8][12][];
Age[][][][][] Aquarius = new Age[6][][][][];
for (int d1 = 0; d1 < Aquarius.length; d1++) {
Aquarius[d1] = new Age[10][][][];
for (int d2 = 0; d2 < Aquarius[d1].length; d2++) {
Aquarius[d1][d2] = new Age[8][][];
for (int d3 = 0; d3 < Aquarius[d1][d2].length; d3++) {
Aquarius[d1][d2][d3] = new Age[12][];
}
}
}
new expression actually creates one array of length 6, 6 arrays of length 10, 6 x 10 = 60 arrays of length 8, and 6 x 10 x 8 = 480 arrays of length 12. This example leaves the fifth dimension, which would be arrays containing the actual array elements (references to Age objects), initialized only to null references. These arrays can be filled in later by other code, such as:
Age[] Hair = { new Age("quartz"), new Age("topaz") };
Aquarius[1][9][6][9] = Hair;
A multidimensional array need not have arrays of the same length at each level.
Thus, a triangular matrix may be created by:
float triang[][] = new float[100][];
for (int i = 0; i < triang.length; i++)
triang[i] = new float[i+1];
Thus:
class Test {
public static void main(String[] args) {
int i = 4;
int ia[][] = new int[i][i=3];
System.out.println(
"[" + ia.length + "," + ia[0].length + "]");
}
}
because the first dimension is calculated as[4,3]
4 before the second dimension expression sets i to 3.If evaluation of a dimension expression completes abruptly, no part of any dimension expression to its right will appear to have been evaluated. Thus, the example:
class Test {
public static void main(String[] args) {
int[][] a = { { 00, 01 }, { 10, 11 } };
int i = 99;
try {
a[val()][i = 1]++;
} catch (Exception e) {
System.out.println(e + ", i=" + i);
}
}
static int val() throws Exception {
throw new Exception("unimplemented");
}
}
because the embedded assignment that setsjava.lang.Exception: unimplemented, i=99
i to 1 is never executed.OutOfMemoryError is thrown. This check occurs only after evaluation of all dimension expressions has completed normally. So, for example, the test program:
class Test {
public static void main(String[] args) {
int len = 0, oldlen = 0;
Object[] a = new Object[0];
try {
for (;;) {
++len;
Object[] temp = new Object[oldlen = len];
temp[0] = a;
a = temp;
}
} catch (Error e) {
System.out.println(e + ", " + (oldlen==len));
}
}
}
because the out-of-memory condition is detected after the dimension expressionjava.lang.OutOfMemoryError, true
oldlen = len is evaluated.Compare this to class instance creation expressions (§15.9), which detect the out-of-memory condition before evaluating argument expressions (§15.9.6).
super. (It is also possible to refer to a field of the current instance or current class by using a simple name; see §6.5.6.)
FieldAccess:
Primary . Identifier
super . Identifier
ClassName .super . Identifier
static:
final, then the result is the value of the specified class variable in the class or interface that is the type of the Primary expression.
final, then the result is a variable, namely, the specified class variable in the class that is the type of the Primary expression.
static:
null, then a NullPointerException is thrown.
final, then the result is the value of the specified instance variable in the object referenced by the value of the Primary.
final, then the result is a variable, namely, the specified instance variable in the object referenced by the value of the Primary.
Thus, the example:
class S { int x = 0; }
class T extends S { int x = 1; }
class Test {
public static void main(String[] args) {
T t = new T();
System.out.println("t.x=" + t.x + when("t", t));
S s = new S();
System.out.println("s.x=" + s.x + when("s", s));
s = t;
System.out.println("s.x=" + s.x + when("s", s));
}
static String when(String name, Object t) {
return " when " + name + " holds a "
+ t.getClass() + " at run time.";
}
}
The last line shows that, indeed, the field that is accessed does not depend on the run-time class of the referenced object; even ift.x=1 when t holds a class T at run time. s.x=0 when s holds a class S at run time. s.x=0 when s holds a class T at run time.
s holds a reference to an object of class T, the expression s.x refers to the x field of class S, because the type of the expression s is S. Objects of class T contain two fields named x, one for class T and one for its superclass S.This lack of dynamic lookup for field accesses allows programs to be run efficiently with straightforward implementations. The power of late binding and overriding is available, but only when instance methods are used. Consider the same example using instance methods to access the fields:
class S { int x = 0; int z() { return x; } }
class T extends S { int x = 1; int z() { return x; } }
class Test {
public static void main(String[] args) {
T t = new T();
System.out.println("t.z()=" + t.z() + when("t", t));
S s = new S();
System.out.println("s.z()=" + s.z() + when("s", s));
s = t;
System.out.println("s.z()=" + s.z() + when("s", s));
}
static String when(String name, Object t) {
return " when " + name + " holds a "
+ t.getClass() + " at run time.";
}
}
The last line shows that, indeed, the method that is accessed does depend on the run-time class of referenced object; whent.z()=1 when t holds a class T at run time. s.z()=0 when s holds a class S at run time. s.z()=1 when s holds a class T at run time.
s holds a reference to an object of class T, the expression s.z() refers to the z method of class T, despite the fact that the type of the expression s is S. Method z of class T overrides method z of class S.The following example demonstrates that a null reference may be used to access a class (static) variable without causing an exception:
class Test {
static String mountain = "Chocorua";
static Test favorite(){
System.out.print("Mount ");
return null;
}
public static void main(String[] args) {
System.out.println(favorite().mountain);
}
}
Mount Chocorua
Even though the result of favorite() is null, a NullPointerException is not thrown. That "Mount " is printed demonstrates that the Primary expression is indeed fully evaluated at run time, despite the fact that only its type, not its value, is used to determine which field to access (because the field mountain is static).
super are valid only in an instance method, instance initializer or constructor, or in the initializer of an instance variable of a class; these are exactly the same situations in which the keyword this may be used (§15.8.3). The forms involving super may not be used anywhere in the class Object, since Object has no superclass; if super appears in class Object, then a compile-time error results.
Suppose that a field access expression super.name appears within class C, and the immediate superclass of C is class S. Then super.name is treated exactly as if it had been the expression ((S)this).name; thus, it refers to the field named name of the current object, but with the current object viewed as an instance of the superclass. Thus it can access the field named name that is visible in class S, even if that field is hidden by a declaration of a field named name in class C.
The use of super is demonstrated by the following example:
interface I { int x = 0; }
class T1 implements I { int x = 1; }
class T2 extends T1 { int x = 2; }
class T3 extends T2 {
int x = 3;
void test() {
System.out.println("x=\t\t"+x);
System.out.println("super.x=\t\t"+super.x);
System.out.println("((T2)this).x=\t"+((T2)this).x);
System.out.println("((T1)this).x=\t"+((T1)this).x);
System.out.println("((I)this).x=\t"+((I)this).x);
}
}
class Test {
public static void main(String[] args) {
new T3().test();
}
}
x= 3 super.x= 2 ((T2)this).x= 2 ((T1)this).x= 1 ((I)this).x= 0
Within class T3, the expression super.x is treated exactly as if it were:
Suppose that a field access expression T.((T2)this).x
super.name appears within class C, and the immediate superclass of the class denoted by T is a class whose fully qualified name is S. Then T.super.name is treated exactly as if it had been the expression ((S)T.this).name.
Thus the expression T.super.name can access the field named name that is visible in the class named by S, even if that field is hidden by a declaration of a field named name in the class named by T.
It is a compile-time error if the current class is not an inner class of class T or T itself.
MethodInvocation:
MethodName ( ArgumentListopt )
Primary . NonWildTypeArgumentsopt Identifier ( ArgumentListopt )
super . NonWildTypeArgumentsopt Identifier ( ArgumentListopt )
ClassName . super . NonWildTypeArgumentsopt Identifier ( ArgumentListopt
)
TypeName . NonWildTypeArguments Identifier ( ArgumentListopt )
ArgumentList:
Expression
ArgumentList , Expression
Resolving a method name at compile time is more complicated than resolving a field name because of the possibility of method overloading. Invoking a method at run time is also more complicated than accessing a field because of the possibility of instance method overriding.
Determining the method that will be invoked by a method invocation expression involves several steps. The following three sections describe the compile-time processing of a method invocation; the determination of the type of the method invocation expression is described in §15.12.3.
. Identifier, then the name of the method is the Identifier and the class to search is the one named by the TypeName. If TypeName is the name of an interface rather than a class, then a compile-time error occurs, because this form can invoke only static methods and interfaces have no static methods.
. Identifier; then the name of the method is the Identifier and the class or interface to search is the declared type T of the field named by the FieldName, if T is a class or interface type, or the upper bound of T if T is a type variable.
super.NonWildTypeArgumentsopt Identifier, then the name of the method is the Identifier and the class to be searched is the superclass of the class whose declaration contains the method invocation. Let T be the type declaration immediately enclosing the method invocation. It is a compile-time error if any of the following situations occur:
super.NonWildTypeArgumentsopt Identifier, then the name of the method is the Identifier and the class to be searched is the superclass of the class C denoted by ClassName. It is a compile-time error if C is not a lexically enclosing class of the current class. It is a compile-time error if C is the class Object. Let T be the type declaration immediately enclosing the method invocation. It is a compile-time error if any of the following situations occur:
static methods and interfaces have no static methods.
A method is applicable if it is either applicable by subtyping (§15.12.2.2), applicable by method invocation conversion (§15.12.2.3), or it is an applicable variable arity method (§15.12.2.4).
The process of determining applicability begins by determining the potentially applicable methods (§15.12.2.1). The remainder of the process is split into three phases.
Discussion
The purpose of the division into phases is to ensure compatibility with older versions of the Java programming language.
The first phase (§15.12.2.2) performs overload resolution without permitting boxing or unboxing conversion, or the use of variable arity method invocation. If no applicable method is found during this phase then processing continues to the second phase.
Discussion
This guarantees that any calls that were valid in older versions of the language are not considered ambiguous as a result of the introduction of variable arity methods, implicit boxing and/or unboxing.
The second phase (§15.12.2.3) performs overload resolution while allowing boxing and unboxing, but still precludes the use of variable arity method invocation. If no applicable method is found during this phase then processing continues to the third phase.
Discussion
This ensures that a variable arity method is never invoked if an applicable fixed arity method exists.
The third phase (§15.12.2.4) allows overloading to be combined with variable arity methods, boxing and unboxing.
Deciding whether a method is applicable will, in the case of generic methods (§8.4.4), require that actual type arguments be determined. Actual type arguments may be passed explicitly or implicitly. If they are passed implicitly, they must be inferred (§15.12.2.7) from the types of the argument expressions.
If several applicable methods have been identified during one of the three phases of applicability testing, then the most specific one is chosen, as specified in section §15.12.2.5. See the following subsections for details.
Discussion
The clause above implies that a non-generic method may be potentially applicable to an invocation that supplies explicit type parameters. Indeed, it may turn out to be applicable. In such a case, the type parameters will simply be ignored.
This rule stems from issues of compatibility and principles of substitutability. Since interfaces or superclasses may be generified independently of their subtypes, we may override a generic method with a non-generic one. However, the overriding (non-generic) method must be applicable to calls to the generic method, including calls that explicitly pass type parameters. Otherwise the subtype would not be substitutable for its generified supertype.
Whether a member method is accessible at a method invocation depends on the access modifier (public, none, protected, or private) in the member's declaration and on where the method invocation appears.
The class or interface determined by compile-time step 1 (§15.12.1) is searched for all member methods that are potentially applicable to this method invocation; members inherited from superclasses and superinterfaces are included in this search.
In addition, if the method invocation has, before the left parenthesis, a MethodName of the form Identifier, then the search process also examines all methods that are (a) imported by single-static-import declarations (§7.5.3) and static-import-on-demand declarations (§7.5.4) within the compilation unit (§7.3) within which the method invocation occurs, and (b) not shadowed (§6.3.1) at the place where the method invocation appears.
If the search does not yield at least one method that is potentially applicable, then a compile-time error occurs.
 i
i n. Then:
n. Then:
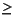 1, be the formal type parameters of m, and let Bl be the declared bound of Rl, 1
1, be the formal type parameters of m, and let Bl be the declared bound of Rl, 1 l
l p. Then:
p. Then:
 i
i n.
n.
Then let Si = Fi[R1 = U1, ..., Rp = Up] 1 i
i n, be the types inferred for of the formal parameters of m.
n, be the types inferred for of the formal parameters of m.
 i
i n, either:
n, either:
 l
l p.
p.
 i
i n. Then:
n. Then:
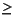 1, be the formal type parameters of m, and let Bl be the declared bound of Rl, 1
1, be the formal type parameters of m, and let Bl be the declared bound of Rl, 1 l
l p. Then:
p. Then:
 i
i n.
n.
Then let Si = Fi[R1 = U1, ..., Rp = Up] 1 i
i n, be the types inferred for the formal parameters of m.
n, be the types inferred for the formal parameters of m.
 i
i n, the type of ei, Ai, can be converted by method invocation conversion (§5.3) to Si.
n, the type of ei, Ai, can be converted by method invocation conversion (§5.3) to Si.
 l
l p.
p.
 i
i k. Then:
k. Then:
 n
n k+1, be the types of the formal parameters of m, where Fn = T[] for some type T, and let R1 ... Rp p
k+1, be the types of the formal parameters of m, where Fn = T[] for some type T, and let R1 ... Rp p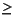 1, be the formal type parameters of m, and let Bl be the declared bound of Rl, 1
1, be the formal type parameters of m, and let Bl be the declared bound of Rl, 1 l
l p. Then:
p. Then:
 i
i n and the constraints Aj << T, n
n and the constraints Aj << T, n j
j k.
k.
Then let Si = Fi[R1 = U1, ..., Rp = Up] 1 i
i n, be the types inferred for the formal parameters of m.
n, be the types inferred for the formal parameters of m.
 k+1, be the types of the formal parameters of m.
k+1, be the types of the formal parameters of m.
 i
i n, the type of ei, Ai, can be converted by method invocation conversion to Si.
n, the type of ei, Ai, can be converted by method invocation conversion to Si.
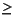 n, then for n
n, then for n i
i k, the type of ei, Ai, can be converted by method invocation conversion to the component type of Sn.
k, the type of ei, Ai, can be converted by method invocation conversion to the component type of Sn.
 l
l p.
p.
The informal intuition is that one method is more specific than another if any invocation handled by the first method could be passed on to the other one without a compile-time type error.
One fixed-arity member method named m is more specific than another member method of the same name and arity if all of the following conditions hold:
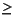 1, be its formal type parameters, let Bl be the declared bound of Rl, 1
1, be its formal type parameters, let Bl be the declared bound of Rl, 1 l
l p, let A1 ... Ap be the actual type arguments inferred (§15.12.2.7) for this invocation under the initial constraints Ti << Ui, 1
p, let A1 ... Ap be the actual type arguments inferred (§15.12.2.7) for this invocation under the initial constraints Ti << Ui, 1 i
i n and let Si = Ui[R1 = A1, ..., Rp = Ap] 1
n and let Si = Ui[R1 = A1, ..., Rp = Ap] 1 i
i n; otherwise let Si = Ui 1
n; otherwise let Si = Ui 1 i
i n.
n.
 l
l p.
p.
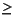 k. The types of the parameters of the first member method are T1, . . . , Tn-1 , Tn[], the types of the parameters of the other method are U1, . . . , Uk-1, Uk[]. If the second method is generic then let R1 ... Rp p
k. The types of the parameters of the first member method are T1, . . . , Tn-1 , Tn[], the types of the parameters of the other method are U1, . . . , Uk-1, Uk[]. If the second method is generic then let R1 ... Rp p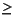 1, be its formal type parameters, let Bl be the declared bound of Rl, 1
1, be its formal type parameters, let Bl be the declared bound of Rl, 1 l
l p, let A1 ... Ap be the actual type arguments inferred (§15.12.2.7) for this invocation under the initial constraints Ti << Ui,1
p, let A1 ... Ap be the actual type arguments inferred (§15.12.2.7) for this invocation under the initial constraints Ti << Ui,1 i
i k-1, Ti << Uk, k
k-1, Ti << Uk, k i
i n and let Si = Ui[R1 = A1, ..., Rp = Ap] 1
n and let Si = Ui[R1 = A1, ..., Rp = Ap] 1 i
i k; otherwise let Si = Ui, 1
k; otherwise let Si = Ui, 1 i
i k. Then:
k. Then:
 l
l p.
p.
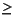 k. The types of the parameters of the first method are U1, . . . , Uk-1, Uk[], the types of the parameters of the other method are T1, . . ., Tn-1, Tn[]. If the second method is generic then let R1 ... Rp p
k. The types of the parameters of the first method are U1, . . . , Uk-1, Uk[], the types of the parameters of the other method are T1, . . ., Tn-1, Tn[]. If the second method is generic then let R1 ... Rp p 1, be its formal type parameters, let Bl be the declared bound of Rl, 1
1, be its formal type parameters, let Bl be the declared bound of Rl, 1 l
l p, let A1 ... Ap be the actual type arguments inferred (§15.12.2.7) for this invocation under the initial constraints Ui << Ti, 1
p, let A1 ... Ap be the actual type arguments inferred (§15.12.2.7) for this invocation under the initial constraints Ui << Ti, 1 i
i k-1, Uk << Ti, k
k-1, Uk << Ti, k i
i n and let Si = Ti[R1 = A1, ..., Rp = Ap] 1
n and let Si = Ti[R1 = A1, ..., Rp = Ap] 1 i
i n; otherwise let Si = Ti, 1
n; otherwise let Si = Ti, 1 i
i n. Then:
n. Then:
A method m1 is strictly more specific than another method m2 if and only if m1 is more specific than m2 and m2 is not more specific than m1.
A method is said to be maximally specific for a method invocation if it is accessible and applicable and there is no other method that is applicable and accessible that is strictly more specific.
If there is exactly one maximally specific method, then that method is in fact the most specific method; it is necessarily more specific than any other accessible method that is applicable. It is then subjected to some further compile-time checks as described in §15.12.3.
It is possible that no method is the most specific, because there are two or more methods that are maximally specific. In this case:
abstract, it is the most specific method.
abstract, and the signatures of all of the maximally specific methods have the same erasure (§4.6), then the most specific method is chosen arbitrarily among the subset of the maximally specific methods that have the most specific return type. However, the most specific method is considered to throw a checked exception if and only if that exception or its erasure is declared in the throws clauses of each of the maximally specific methods.
void, then the result is void.
 i
i n, let Fi be the formal type parameters of the method, let Ai be the actual type arguments inferred for the method invocation, and let R be the declared return type of the method being invoked. The result type is obtained by applying capture conversion (§5.1.10) to R[F1 := A1, ..., Fn := An].
n, let Fi be the formal type parameters of the method, let Ai be the actual type arguments inferred for the method invocation, and let R be the declared return type of the method being invoked. The result type is obtained by applying capture conversion (§5.1.10) to R[F1 := A1, ..., Fn := An].
 i
i n, let Fi be the formal type parameters of the method, let Ai be the actual type arguments inferred for the method invocation, and let Ej, 1
n, let Fi be the formal type parameters of the method, let Ai be the actual type arguments inferred for the method invocation, and let Ej, 1 j
j m be the exception types declared in the throws clause of the method being invoked. The throws clause consists of the types to Ej[F1 := A1, ..., Fn := An].
m be the exception types declared in the throws clause of the method being invoked. The throws clause consists of the types to Ej[F1 := A1, ..., Fn := An].
Discussion
The process of type inference is inherently complex. Therefore, it is useful to give an informal overview of the process before delving into the detailed specification.
Inference begins with an initial set of constraints. Generally, the constraints require that the statically known types of the actual arguments are acceptable given the declared formal argument types. We discuss the meaning of "acceptable" below.
Given these initial constraints, one may derive a set of supertype and/or equality constraints on the formal type parameters of the method or constructor.
Next, one must try and find a solution that satisfies the constraints on the type parameters. As a first approximation, if a type parameter is constrained by an equality constraint, then that constraint gives its solution. Bear in mind that the constraint may equate one type parameter with another, and only when the entire set of constraints on all type variables is resolved will we have a solution.
A supertype constraint T :> X implies that the solution is one of supertypes of X. Given several such constraints on T, we can intersect the sets of supertypes implied by each of the constraints, since the type parameter must be a member of all of them. We can then choose the most specific type that is in the intersection.
Computing the intersection is more complicated than one might first realize. Given that a type parameter is constrained to be a supertype of two distinct invocations of a generic type, say List<Object> and List<String>, the naive intersection operation might yield Object. However, a more sophisticated analysis yields a set containing List<?>. Similarly, if a type parameter, T, is constrained to be a supertype of two unrelated interfaces I and J, we might infer T must be Object, or we might obtain a tighter bound of I & J. These issues are discussed in more detail later in this section.
We will use the following notational conventions in this section:
Discussion
In a simpler world, the constraints could be of the form A <: F - simply requiring that the actual argument types be subtypes of the formal ones. However, reality is more involved. As discussed earlier, method applicability testing consists of up to three phases; this is required for compatibility reasons. Each phase imposes slightly different constraints. If a method is applicable by subtyping (§15.12.2.2), the constraints are indeed subtyping constraints. If a method is applicable by method invocation conversion (§15.12.2.3), the constraints imply that the actual type is convertible to the formal type by method invocation conversion. The situation is similar for the third phase (§15.12.2.4), but the exact form of the constraints differ due to the variable arity.
These constraints are then reduced to a set of simpler constraints of the forms T :> X, T = X or T <: X, where T is a type parameter of the method. This reduction is achieved by the procedure given below:
Discussion
It may be that the initial constraints are unsatisfiable; we say that inference is overconstrained. In that case, we do not necessarily derive unsatisfiable constraints on the type parameters. Instead, we may infer actual type arguments for the invocation, but once we substitute the actual type arguments for the formal type parameters, the applicability test may fail because the actual argument types are not acceptable given the substituted formals.
An alternative strategy would be to have type inference itself fail in such cases. Compilers may choose to do so, provided the effect is equivalent to that specified here.
Given a constraint of the form A << F, A = F, or A >> F:
null, no constraint is implied on Tj.
Discussion
This follows from the covariant subtype relation among array types. The constraint A << F, in this case means that A << U[]. A is therefore necessarily an array type V[], or a type variable whose upper bound is an array type V[] - otherwise the relation A << U[] could never hold true. It follows that V[] << U[]. Since array subtyping is covariant, it must be the case that V << U.
 k
k n where U is a type expression that involves Tj, then if A has a supertype of the form G<..., Xk-1, V, Xk+1, ...> where V is a type expression, this algorithm is applied recursively to the constraint V = U.
n where U is a type expression that involves Tj, then if A has a supertype of the form G<..., Xk-1, V, Xk+1, ...> where V is a type expression, this algorithm is applied recursively to the constraint V = U.
Discussion
For simplicity, assume that G takes a single type argument. If the method invocation being examined is to be applicable, it must be the case that A is a subtype of some invocation of G. Otherwise, A << F would never be true.
In other words, A << F, where F = G<U>, implies that A << G<V> for some V. Now, since U is a type expression (and therefore, U is not a wildcard type argument), it must be the case that U = V, by the non-variance of ordinary parameterized type invocations.
The formulation above merely generalizes this reasoning to generics with an arbitrary number of type arguments.
Discussion
Again, let's keep things as simple as possible, and consider only the case where G has a single type argument.
A <<F in this case means A << G<? extends U>. As above, it must be the case that A is a subtype of some invocation of G. However, A may now be a subtype of either G<V>, or G<? extends V>, or G<? super V>. We examine these cases in turn. The first variation is described (generalized to multiple arguments) by the sub-bullet directly above. We therefore have A = G<V> << G<? extends U>. The rules of subtyping for wildcards imply that V << U.
Discussion
Extending the analysis above, we have A = G<? extends V> << G<? extends U>. The rules of subtyping for wildcards again imply that V << U.
Discussion
Here, we have A = G<? super V> << G<? extends U>. In general, we cannot conclude anything in this case. However, it is not necessarily an error. It may be that U will eventually be inferred to beObject, in which case the call may indeed be valid. Therefore, we simply refrain from placing any constraint on U.
Discussion
As usual, we consider only the case where G has a single type argument.
A <<F in this case means A << G<? super U>. As above, it must be the case that A is a subtype of some invocation of G. A may now be a subtype of either G<V>, or G<? extends V>, or G<? super V>. We examine these cases in turn. The first variation is described (generalized to multiple arguments) by the sub-bullet directly above. We therefore have A = G<V> << G<? super U>. The rules of subtyping for wildcards imply that V >> U.
Discussion
We have A = G<? super V> << G<? super U>. The rules of subtyping for lower-bounded wildcards again imply that V >> U.
Discussion
Here, we have A = G<? extends V> << G<? super U>. In general, we cannot conclude anything in this case. However, it is not necessarily an error. It may be that U will eventually be inferred to the null type, in which case the call may indeed be valid. Therefore, we simply refrain from placing any constraint on U.
Discussion
Such a constraint is never part of the initial constraints. However, it can arise as the algorithm recurses. We have seen this occur above, when the constraint A << F relates two parameterized types, as in G<V> << G<U>.
Discussion
Clearly, if the array types U[] and V[] are the same, their component types must be the same.
 k
k n where U is type expression that involves Tj, then if A is of the form G<..., Xk-1, V, Xk+1,...> where V is a type expression, this algorithm is applied recursively to the constraint V = U.
n where U is type expression that involves Tj, then if A is of the form G<..., Xk-1, V, Xk+1,...> where V is a type expression, this algorithm is applied recursively to the constraint V = U.
Discussion
Such situations arise when the algorithm recurses, due to the contravariant subtyping rules associated with lower-bounded wildcards (those of the form G<? super X>).
It might be tempting to consider A>> F as being the same as F << A, but the problem of inference is not symmetric. We need to remember which participant in the relation includes a type to be inferred.
Discussion
We do not make use of such constraints in the main body of the inference algorithm. However, they are used in section §15.12.2.8.
Discussion
This follows from the covariant subtype relation among array types. The constraint A >> F, in this case means that A >> U[]. A is therefore necessarily an array type V[], or a type variable whose upper bound is an array type V[] - otherwise the relation A >> U[] could never hold true. It follows that V[] >> U[]. Since array subtyping is covariant, it must be the case that V >> U.
Discussion
In this case (once again restricting the analysis to the unary case), we have the constraint A >> F = G<U>. A must be a supertype of the generic type G. However, since A is not a parameterized type, it cannot depend upon the type argument U in any way. It is a supertype of G<X> for every X that is a valid type argument to G. No meaningful constraint on U can be derived from A.
Discussion
Our goal here is to simplify the relationship between A and F. We aim to recursively invoke the algorithm on a simpler case, where the actual type argument is known to be an invocation of the same generic type declaration as the formal.
Let's consider the case where both H and G have only a single type argument. Since we have the constraint A = H<X> >> F = G<U>, where H is distinct from G, it must be the case that H is some proper superclass or superinterface of G. There must be a (non-wildcard) invocation of H that is a supertype of F = G<U>. Call this invocation V.
If we replace F by V in the constraint, we will have accomplished the goal of relating two invocations of the same generic (as it happens, H).
How do we compute V? The declaration of G must introduce a formal type parameter S, and there must be some (non-wildcard) invocation of H, H<U1>, that is a supertype of G<S>. Substituting the type expression U for S will then yield a (non-wildcard) invocation of H, H<U1>[S = U], that is a supertype of G<U>. For example, in the simplest instance, U1 might be S, in which case we have G<S> <: H<S>, and G<U> <: H<U> = H<S>[S = U] = V.
It may be the case that H<U1> is independent of S - that is, S does not occur in U1 at all. However, the substitution described above is still valid - in this situation, V = H<U1>[S = U] = H<U1>. Furthermore, in this circumstance, G<T> <: H<U1> for any T, and in particular G<U> <: H<U1> = V.
Regardless of whether U1 depends on S, we have determined the type V, the invocation of H that is a supertype of G<U>. We can now invoke the algorithm recursively on the constraint H<X> = A >> V = H<U1>[S = U]. We will then be able to relate the type arguments of both invocations of H and extract the relevant constraints from them.
Discussion
We have A = G<W> >> F = G<U> for some type expression W. Since W is a type expression (and not a wildcard type argument), it must be the case that W = U, by the non-variance of parameterized types.
Discussion
We have A = G<? extends W> >> F = G<U> for some type expression W. It must be the case that W >> U, by the subtyping rules for wildcard types.
We have A = G<? super W> >> F = G<U> for some type expression W. It must be the case that W << U, by the subtyping rules for wildcard types.
Discussion
Once again restricting the analysis to the unary case, we have the constraint A >> F = G<? extends U>. A must be a supertype of the generic type G. However, since A is not a parameterized type, it cannot depend upon U in any way. It is a supertype of the type G<? extends X> for every X such that ? extends X is a valid type argument to G. No meaningful constraint on U can be derived from A.
Discussion
Our goal here is once more to simplify the relationship between A and F, and recursively invoke the algorithm on a simpler case, where the actual type argument is known to be an invocation of the same generic type as the formal.
Assume both H and G have only a single type argument. Since we have the constraint A = H<X> >> F = G<? extends U>, where H is distinct from G, it must be the case that H is some proper superclass or superinterface of G. There must be an invocation of
How do we compute H<Y>? As before, note that the declaration of G must introduce a formal type parameter S, and there must be some (non-wildcard) invocation of H, H<U1>, that is a supertype of G<S>. However, substituting ? extends U for S is not generally valid. To see this, assume U1 = T[].
Instead, we produce an invocation of H, H<? extends U1>[S = U]. In the simplest instance, U1 might be S, in which case we have G<S> <: H<S>, and G<? extends U> <: H<? extends U> = H<? extends S>[S = U] = V.
Discussion
We have A = G<? extends W> >> F = G<? extends U> for some type expression W. By the subtyping rules for wildcards it must be the case that W >> U.
Discussion
Restricting the analysis to the unary case, we have the constraint A >> F = G<? super U>. A must be a supertype of the generic type G. However, since A is not a parameterized type, it cannot depend upon U in any way. It is a supertype of the type G<? super X> for every X such that ? super X is a valid type argument to G. No meaningful constraint on U can be derived from A.
Discussion
The treatment here is analogous to the case where A = G<? extends U>. Here our example would produce an invocation H<? super U1>[S = U]
Discussion
We have A = G<? super W> >> F = G<? super U> for some type expression W. It must be the case that W << U, by the subtyping rules for wildcard types.
Discussion
This concludes the process of determining constraints on the formal type parameters of a method.
Note that this process does not impose any constraints on the type parameters based on their declared bounds. Once the actual type arguments are inferred, they will be tested against the declared bounds of the formal type parameters as part of applicability testing.
Note also that type inference does not affect soundness in any way. If the types inferred are nonsensical, the invocation will yield a type error. The type inference algorithm should be viewed as a heuristic, designed to perfdorm well in practice. If it fails to infer the desired result, explicit type paramneters may be used instead.
Next, for each type variable Tj, 1
For each implied equality constraint Tj = U or U = Tj:
For a type U, we write ST(U) for the set of supertypes of U, and define the erased supertype set of U,
EST(U) = { V | W in ST(U) and V = |W| }
where |W| is the erasure (§4.6) of W.
Discussion
The reason for computing the set of erased supertypes is to deal with situations where a type variable is constrained to be a supertype of several distinct invocations of a generic type declaration, For example, if T :> List<String> and T :> List<Object>, simply intersecting the sets ST(List<String>) = {List<String>, Collection<String>, Object} and ST(List<Object>) = {List<Object>), Collection<Object>, Object} would yield a set {Object}, and we would have lost track of the fact that T can safely be assumed to be a List.
In contrast, intersecting EST(List<String>) = {List, Collection, Object} and EST(List<Object>) = {List, Collection, Object} yields {List, Collection, Object}, which we will eventually enable us to infer T = List<?> as described below.
The erased candidate set for type parameter Tj , EC, is the intersection of all the sets EST(U) for each U in U1 .. Uk. The minimal erased candidate set for Tj is
MEC = { V | V in EC, and for all W
Discussion
Because we are seeking to infer more precise types, we wish to filter out any candidates that are supertypes of other candidates. This is what computing MEC accomplishes.
In our running example, we had EC = {List, Collection, Object}, and now MEC = {List}.
The next step will be to recover actual type arguments for the inferred types.
For any element G of MEC that is a generic type declaration, define the relevant invocations of G, Inv(G) to be:
Inv(G) = { V | 1
Discussion
In our running example, the only generic element of MEC is List, and Inv(List) = {List<String>, List<Object>}. We now will seek to find a type argument for List that contains (§4.5.1.1) both String and Object.
This is done by means of the least containing invocation (lci) operation defined below. The first line defines lci() on a set, such as Inv(List), as an operation on a list of the elements of the set. The next line defines the operation on such lists, as a pairwise reduction on the elements of the list. The third line is the definition of lci() on pairs of parameterized types, which in turn relies on the notion of least containing type argument (lcta).
lcta() is defined for all six possible cases. Then CandidateInvocation(G) defines the most specific invocation of the generic G that is contains all the invocations of G that are known to be supertypes of Tj. This will be our candidate invocation of G in the bound we infer for Tj .
and let CandidateInvocation(G) = lci(Inv(G)) where lci, the least containing invocation is defined
lci(S) = lci(e1, ..., en) where ei in S, 1
where lcta() is the the least containing type argument function defined (assuming U and V are type expressions) as:
lcta(U, V) = U if U = V, ? extends lub(U, V) otherwise
where glb() is as defined in (§5.1.10).
Discussion
Finally, we define a bound for Tj based on on all the elements of the minimal erased candidate set of its supertypes. If any of these elements are generic, we use the CandidateInvocation() function to recover the type argument information.
Then, define Candidate(W) = CandidateInvocation(W) if W is generic, W otherwise.
Then the inferred type for Tj is
lub(U1 ... Uk) = Candidate(W1) & ... & Candidate(Wr) where Wi, 1
It is possible that the process above yields an infinite type. This is permissible, and Java compilers must recognize such situations and represent them appropriately using cyclic data structures.
Discussion
The possibility of an infinite type stems from the recursive calls to lub().
Readers familiar with recursive types should note that an infinite type is not the same as a recursive type.
Any remaining type variables that have not yet been inferred are then inferred to have type
In the example program: Another example is: If the method
If a third definition of
So, for example, consider two compilation units, one for class
The application programmer who coded class Notice, by the way, that the most specific method (indeed, the only applicable method) for the method invocation of Suppose the programmer reported this software error and the maintainer of the If the application programmer then runs the old binary file for
With forethought about such problems, the maintainer of the Ideally, source code should be recompiled whenever code that it depends on is changed. However, in an environment where different classes are maintained by different organizations, this is not always feasible. Defensive programming with careful attention to the problems of class evolution can make upgraded code much more robust. See §13 for a detailed discussion of binary compatibility and type evolution.
In either case, if the evaluation of the Primary expression completes abruptly, then no part of any argument expression appears to have been evaluated, and the method invocation completes abruptly for the same reason.
If the method being invoked is a variable arity method (§8.4.1) m, it necessarily has n>0 formal parameters. The final formal parameter of m necessarily has type T[] for some T, and m is necessarily being invoked with k
If m is being invoked with k
The argument expressions (possibly rewritten as described above) are now evaluated to yield argument values. Each argument value corresponds to exactly one of the method's n formal parameters.
The argument expressions, if any, are evaluated in order, from left to right. If the evaluation of any argument expression completes abruptly, then no part of any argument expression to its right appears to have been evaluated, and the method invocation completes abruptly for the same reason.The result of evaluating the jth argument expression is the jth argument value, for 1
The implementation must also insure, during linkage, that the type T and the method m are accessible. For the type T:
If the invocation mode is
Otherwise, an instance method is to be invoked and there is a target reference. If the target reference is
If the invocation mode is
Otherwise, the invocation mode is
Let X be the compile-time type of the target reference of the method invocation.
The above procedure will always find a non-abstract, accessible method to invoke, provided that all classes and interfaces in the program have been consistently compiled. However, if this is not the case, then various errors may occur. The specification of the behavior of a Java virtual machine under these circumstances is given by The Java Virtual Machine Specification.We note that the dynamic lookup process, while described here explicitly, will often be implemented implicitly, for example as a side-effect of the construction and use of per-class method dispatch tables, or the construction of other per-class structures used for efficient dispatch.
Now a new activation frame is created, containing the target reference (if any) and the argument values (if any), as well as enough space for the local variables and stack for the method to be invoked and any other bookkeeping information that may be required by the implementation (stack pointer, program counter, reference to previous activation frame, and the like). If there is not sufficient memory available to create such an activation frame, an
The newly created activation frame becomes the current activation frame. The effect of this is to assign the argument values to corresponding freshly created parameter variables of the method, and to make the target reference available as
If the erasure of the type of the method being invoked differs in its signature from the erasure of the type of the compile-time declaration for the method invocation (§15.12.3), then if any of the argument values is an object which is not an instance of a subclass or subinterface of the erasure of the corresponding formal parameter type in the compile-time declaration for the method invocation, then a
Discussion
As an example of such a situation, consider the declarations:
Such situations can only arise if the program gives rise to an unchecked warning (§5.1.9).
Implementations can enforce these semantics by creating bridge methods. In the above example, the following bridge method would be created in class
If the method m is a
If the method m is not
If the method m is
So, for example, in:
This method is then invoked whenever the target object for an invocation of
Overriding is sometimes called "late-bound self-reference"; in this example it means that the reference to When accessing an instance variable,
The casts to types
The type of the array reference expression must be an array type (call it T[], an array whose components are of type T) or a compile-time error results. Then the type of the array access expression is the result of applying capture conversion (§5.1.10) to T.
The index expression undergoes unary numeric promotion (§); the promoted type must be
The result of an array reference is a variable of type T, namely the variable within the array selected by the value of the index expression. This resulting variable, which is a component of the array, is never considered
Thus, the example:
If evaluation of the expression to the left of the brackets completes abruptly, no part of the expression within the brackets will appear to have been evaluated. Thus, the example:
If the array reference expression produces
A
At run time, if evaluation of the operand expression completes abruptly, then the postfix increment expression completes abruptly for the same reason and no incrementation occurs. Otherwise, the value
Note that the binary numeric promotion mentioned above may include unboxing conversion (§5.1.8) and value set conversion (§5.1.13). If necessary, value set conversion is applied to the sum prior to its being stored in the variable.
A variable that is declared
At run time, if evaluation of the operand expression completes abruptly, then the postfix decrement expression completes abruptly for the same reason and no decrementation occurs. Otherwise, the value
Note that the binary numeric promotion mentioned above may include unboxing conversion (§5.1.8) and value set conversion (§5.1.13). If necessary, value set conversion is applied to the difference prior to its being stored in the variable.
A variable that is declared
At run time, if evaluation of the operand expression completes abruptly, then the prefix increment expression completes abruptly for the same reason and no incrementation occurs. Otherwise, the value
Note that the binary numeric promotion mentioned above may include unboxing conversion (§5.1.8) and value set conversion (§5.1.13). If necessary, value set conversion is applied to the sum prior to its being stored in the variable.
A variable that is declared
At run time, if evaluation of the operand expression completes abruptly, then the prefix decrement expression completes abruptly for the same reason and no decrementation occurs. Otherwise, the value
Note that the binary numeric promotion mentioned above may include unboxing conversion (§5.1.8) and value set conversion (§5.1.13). If necessary, format conversion is applied to the difference prior to its being stored in the variable.
A variable that is declared
At run time, the value of the unary plus expression is the promoted value of the operand.
Note that unary numeric promotion performs value set conversion (§5.1.13). Whatever value set the promoted operand value is drawn from, the unary negation operation is carried out and the result is drawn from that same value set. That result is then subject to further value set conversion.
At run time, the value of the unary minus expression is the arithmetic negation of the promoted value of the operand.
For integer values, negation is the same as subtraction from zero. The Java programming language uses two's-complement representation for integers, and the range of two's-complement values is not symmetric, so negation of the maximum negative
For floating-point values, negation is not the same as subtraction from zero, because if
At run time, the value of the unary bitwise complement expression is the bitwise complement of the promoted value of the operand; note that, in all cases,
At run time, the operand is subject to unboxing conversion (§5.1.8) if necessary; the value of the unary logical complement expression is
See §15.15 for a discussion of the distinction between UnaryExpression and UnaryExpressionNotPlusMinus.
The type of a cast expression is the result of applying capture conversion (§5.1.10) to the type whose name appears within the parentheses. (The parentheses and the type they contain are sometimes called the cast operator.) The result of a cast expression is not a variable, but a value, even if the result of the operand expression is a variable.
A cast operator has no effect on the choice of value set (§4.2.3) for a value of type
It is a compile-time error if the compile-time type of the operand may never be cast to the type specified by the cast operator according to the rules of casting conversion (§5.5). Otherwise, at run-time, the operand value is converted (if necessary) by casting conversion to the type specified by the cast operator. Some casts result in an error at compile time. Some casts can be proven, at compile time, always to be correct at run time. For example, it is always correct to convert a value of a class type to the type of its superclass; such a cast should require no special action at run time. Finally, some casts cannot be proven to be either always correct or always incorrect at compile time. Such casts require a test at run time. See for §5.5 details.
Note that binary numeric promotion performs unboxing conversion (§5.1.8) and value set conversion (§5.1.13).
If an integer multiplication overflows, then the result is the low-order bits of the mathematical product as represented in some sufficiently large two's-complement format. As a result, if overflow occurs, then the sign of the result may not be the same as the sign of the mathematical product of the two operand values.
The result of a floating-point multiplication is governed by the rules of IEEE 754 arithmetic:
Next, a value must be chosen from the chosen value set to represent the product. If the magnitude of the product is too large to represent, we say the operation overflows; the result is then an infinity of appropriate sign. Otherwise, the product is rounded to the nearest value in the chosen value set using IEEE 754 round-to-nearest mode. The Java programming language requires support of gradual underflow as defined by IEEE 754 (§4.2.4).
Integer division rounds toward
The result of a floating-point division is determined by the specification of IEEE arithmetic:
Next, a value must be chosen from the chosen value set to represent the quotient. If the magnitude of the quotient is too large to represent, we say the operation overflows; the result is then an infinity of appropriate sign. Otherwise, the quotient is rounded to the nearest value in the chosen value set using IEEE 754 round-to-nearest mode. The Java programming language requires support of gradual underflow as defined by IEEE 754 (§4.2.4).
In C and C++, the remainder operator accepts only integral operands, but in the Java programming language, it also accepts floating-point operands.
The result of a floating-point remainder operation is determined by the rules of IEEE arithmetic:
Examples:
Otherwise, the type of each of the operands of the
In every case, the type of each of the operands of the binary
A value x of primitive type T is first converted to a reference value as if by giving it as an argument to an appropriate class instance creation expression:
Now only reference values need to be considered. If the reference is
The
For primitive types, an implementation may also optimize away the creation of a wrapper object by converting directly from a primitive type to a string.
The + operator is syntactically left-associative, no matter whether it is later determined by type analysis to represent string concatenation or addition. In some cases care is required to get the desired result. For example, the expression:
In this jocular little example:
the method
In the code, note the careful conditional generation of the singular " into two pieces to avoid an inconveniently long line in the source code.
Binary numeric promotion is performed on the operands (§5.6.2). The type of an additive expression on numeric operands is the promoted type of its operands. If this promoted type is
Note that binary numeric promotion performs value set conversion (§5.1.13) and unboxing conversion (§5.1.8).
Addition is a commutative operation if the operand expressions have no side effects. Integer addition is associative when the operands are all of the same type, but floating-point addition is not associative.
If an integer addition overflows, then the result is the low-order bits of the mathematical sum as represented in some sufficiently large two's-complement format. If overflow occurs, then the sign of the result is not the same as the sign of the mathematical sum of the two operand values.
The result of a floating-point addition is determined using the following rules of IEEE arithmetic:
Next, a value must be chosen from the chosen value set to represent the sum. If the magnitude of the sum is too large to represent, we say the operation overflows; the result is then an infinity of appropriate sign. Otherwise, the sum is rounded to the nearest value in the chosen value set using IEEE 754 round-to-nearest mode. The Java programming language requires support of gradual underflow as defined by IEEE 754 (§4.2.4).
Note that, for integer values, subtraction from zero is the same as negation. However, for floating-point operands, subtraction from zero is not the same as negation, because if
Despite the fact that overflow, underflow, or loss of information may occur, evaluation of a numeric additive operator never throws a run-time exception.
If the promoted type of the left-hand operand is
If the promoted type of the left-hand operand is
At run time, shift operations are performed on the two's complement integer representation of the value of the left operand.
The value of
The value of
The value of
Note that binary numeric promotion performs value set conversion (§5.1.13) and unboxing conversion (§5.1.8). Comparison is carried out accurately on floating-point values, no matter what value sets their representing values were drawn from.
The result of a floating-point comparison, as determined by the specification of the IEEE 754 standard, is:
At run time, the result of the
If a cast of the RelationalExpression to the ReferenceType would be rejected as a compile-time error, then the Consider the example program:
The equality operators may be used to compare two operands that are convertible (§5.1.8) to numeric type, or two operands of type
In all cases,
Note that binary numeric promotion performs value set conversion (§5.1.13) and unboxing conversion (§5.1.8). Comparison is carried out accurately on floating-point values, no matter what value sets their representing values were drawn from.
Floating-point equality testing is performed in accordance with the rules of the IEEE 754 standard:
If one of the operands is of type
The result of
The result of
A compile-time error occurs if it is impossible to convert the type of either operand to the type of the other by a casting conversion (§5.5). The run-time values of the two operands would necessarily be unequal.
At run time, the result of
The result of While
For
For
For For example, the result of the expression
For
For
For
At run time, the left-hand operand expression is evaluated first; if the result has type
At run time, the left-hand operand expression is evaluated first; if the result has type Thus,
The conditional operator is syntactically right-associative (it groups right-to-left), so that
The first expression must be of type
Note that it is a compile-time error for either the second or the third operand expression to be an invocation of a
The type of a conditional expression is determined as follows:
At run time, the result of the assignment expression is the value of the variable after the assignment has occurred. The result of an assignment expression is not itself a variable.
A variable that is declared
At run time, the expression is evaluated in one of three ways:
The compiler may be able to prove at compile time that the array component will be of type TC exactly (for example, TC might be
Otherwise, the value of the right-hand operand is converted to the type of the left-hand variable, is subjected to value set conversion (§5.1.13) to the appropriate standard value set (not an extended-exponent value set), and the result of the conversion is stored into the variable.The rules for assignment to an array component are illustrated by the following example program:
For example, the following code is correct:
The rules for compound assignment to an array component are illustrated by the following example program:
The following program illustrates the fact that the value of the left-hand side of a compound assignment is saved before the right-hand side is evaluated:
Unlike C and C++, the Java programming language has no comma operator.
A compile-time constant expression is an expression denoting a value of primitive type or a
A compile-time constant expression is always treated as FP-strict (§15.4), even if it occurs in a context where a non-constant expression would not be considered to be FP-strict. Examples of constant expressions:
Copyright © 1996-2005 Sun Microsystems, Inc.
All rights reserved
 j
j n, the implied equality constraints are resolved as follows:
n, the implied equality constraints are resolved as follows:
Then, for each remaining type variable Tj, the constraints Tj :> U are considered. Given that these constraints are Tj :> U1 ... Tj :> Uk, the type of Tj is inferred as lub(U1 ... Uk), computed as follows: j. Then all constraints involving Tj are rewritten such that Tj is replaced with Tk, and processing continues with the next type variable.
j. Then all constraints involving Tj are rewritten such that Tj is replaced with Tk, and processing continues with the next type variable.
 V in EC, it is not the case that W <: V}
V in EC, it is not the case that W <: V}
 i
i k, V in ST(Ui), V = G<...>}
k, V in ST(Ui), V = G<...>}
 i
i n
n
lci(e1, ..., en) = lci(lci(e1, e2), e3, ..., en)
lci(G<X1, ..., Xn>, G<Y1, ..., Yn>) = G<lcta(X1, Y1),..., lcta(Xn, Yn)>
lcta(U, ? extends V) = ? extends lub(U, V)
lcta(U, ? super V) = ? super glb(U, V)
lcta(? extends U, ? extends V) = ? extends lub(U, V)
lcta(? extends U, ? super V) = U if U = V, ? otherwise
lcta(? super U, ? super V) = ? super glb(U, V)
 i
i r, are the elements of MEC.
r, are the elements of MEC.
15.12.2.8 Inferring Unresolved Type Arguments
If any of the method's type arguments were not inferred from the types of the actual arguments, they are now inferred as follows.
Then, a set of initial constraints consisting of:
is created and used to infer constraints on the type arguments using the algorithm of section (§15.12.2.7). Any equality constraints are resolved, and then, for each remaining constraint of the form Ti <: Uk, the argument Ti is inferred to be glb(U1, ..., Uk) (§5.1.10). void; and
Object
Object.
15.12.2.9 Examples
for the method invocation public class Doubler {
static int two() { return two(1); }
private static int two(int i) { return 2*i; }
}
class Test extends Doubler {
public static long two(long j) {return j+j; }
public static void main(String[] args) {
System.out.println(two(3));
System.out.println(Doubler.two(3)); // compile-time error
}
}
two(1) within class Doubler, there are two accessible methods named two, but only the second one is applicable, and so that is the one invoked at run time. For the method invocation two(3) within class Test, there are two applicable methods, but only the one in class Test is accessible, and so that is the one to be invoked at run time (the argument 3 is converted to type long). For the method invocation Doubler.two(3), the class Doubler, not class Test, is searched for methods named two; the only applicable method is not accessible, and so this method invocation causes a compile-time error.
Here, a compile-time error occurs for the second invocation of class ColoredPoint {
int x, y;
byte color;
void setColor(byte color) { this.color = color; }
}
class Test {
public static void main(String[] args) {
ColoredPoint cp = new ColoredPoint();
byte color = 37;
cp.setColor(color);
cp.setColor(37); // compile-time error
}
}
setColor, because no applicable method can be found at compile time. The type of the literal 37 is int, and int cannot be converted to byte by method invocation conversion. Assignment conversion, which is used in the initialization of the variable color, performs an implicit conversion of the constant from type int to byte, which is permitted because the value 37 is small enough to be represented in type byte; but such a conversion is not allowed for method invocation conversion.setColor had, however, been declared to take an int instead of a byte, then both method invocations would be correct; the first invocation would be allowed because method invocation conversion does permit a widening conversion from byte to int. However, a narrowing cast would then be required in the body of setColor: void setColor(int color) { this.color = (byte)color; }
15.12.2.10 Example: Overloading Ambiguity
Consider the example:
This example produces an error at compile time. The problem is that there are two declarations of test that are applicable and accessible, and neither is more specific than the other. Therefore, the method invocation is ambiguous.class Point { int x, y; }
class ColoredPoint extends Point { int color; }
class Test {
static void test(ColoredPoint p, Point q) {
System.out.println("(ColoredPoint, Point)");
}
static void test(Point p, ColoredPoint q) {
System.out.println("(Point, ColoredPoint)");
}
public static void main(String[] args) {
ColoredPoint cp = new ColoredPoint();
test(cp, cp); // compile-time error
}
}
test were added:
then it would be more specific than the other two, and the method invocation would no longer be ambiguous. static void test(ColoredPoint p, ColoredPoint q) {
System.out.println("(ColoredPoint, ColoredPoint)");
}
15.12.2.11 Example: Return Type Not Considered
As another example, consider:
Here the most specific declaration of method class Point { int x, y; }
class ColoredPoint extends Point { int color; }
class Test {
static int test(ColoredPoint p) {
return p.color;
}
static String test(Point p) {
return "Point";
}
public static void main(String[] args) {
ColoredPoint cp = new ColoredPoint();
String s = test(cp); // compile-time error
}
}
test is the one taking a parameter of type ColoredPoint. Because the result type of the method is int, a compile-time error occurs because an int cannot be converted to a String by assignment conversion. This example shows that the result types of methods do not participate in resolving overloaded methods, so that the second test method, which returns a String, is not chosen, even though it has a result type that would allow the example program to compile without error.15.12.2.12 Example: Compile-Time Resolution
The most applicable method is chosen at compile time; its descriptor determines what method is actually executed at run time. If a new method is added to a class, then source code that was compiled with the old definition of the class might not use the new method, even if a recompilation would cause this method to be chosen.Point:
and one for class package points;
public class Point {
public int x, y;
public Point(int x, int y) { this.x = x; this.y = y; }
public String toString() { return toString(""); }
public String toString(String s) {
return "(" + x + "," + y + s + ")";
}
}
ColoredPoint:
Now consider a third compilation unit that uses package points;
public class ColoredPoint extends Point {
public static final int
RED = 0, GREEN = 1, BLUE = 2;
public static String[] COLORS =
{ "red", "green", "blue" };
public byte color;
public ColoredPoint(int x, int y, int color) {
super(x, y); this.color = (byte)color;
}
/** Copy all relevant fields of the argument into
this ColoredPoint object. */
public void adopt(Point p) { x = p.x; y = p.y; }
public String toString() {
String s = "," + COLORS[color];
return super.toString(s);
}
}
ColoredPoint:
The output is:import points.*;
class Test {
public static void main(String[] args) {
ColoredPoint cp =
new ColoredPoint(6, 6, ColoredPoint.RED);
ColoredPoint cp2 =
new ColoredPoint(3, 3, ColoredPoint.GREEN);
cp.adopt(cp2);
System.out.println("cp: " + cp);
}
}
cp: (3,3,red)
Test has expected to see the word green, because the actual argument, a ColoredPoint, has a color field, and color would seem to be a "relevant field" (of course, the documentation for the package Points ought to have been much more precise!).adopt has a signature that indicates a method of one parameter, and the parameter is of type Point. This signature becomes part of the binary representation of class Test produced by the compiler and is used by the method invocation at run time.points package decided, after due deliberation, to correct it by adding a method to class ColoredPoint:
public void adopt(ColoredPoint p) {
adopt((Point)p); color = p.color;
}
Test with the new binary file for ColoredPoint, the output is still:Test still has the descriptor "one parameter, whose type is Point; void" associated with the method call cp.adopt(cp2). If the source code for Test is recompiled, the compiler will then discover that there are now two applicable adopt methods, and that the signature for the more specific one is "one parameter, whose type is ColoredPoint; void"; running the program will then produce the desired output:cp: (3,3,green)
points package could fix the ColoredPoint class to work with both newly compiled and old code, by adding defensive code to the old adopt method for the sake of old code that still invokes it on ColoredPoint arguments:
public void adopt(Point p) {
if (p instanceof ColoredPoint)
color = ((ColoredPoint)p).color;
x = p.x; y = p.y;
}
15.12.3 Compile-Time Step 3: Is the Chosen Method Appropriate?
If there is a most specific method declaration for a method invocation, it is called the compile-time declaration for the method invocation. Three further checks must be made on the compile-time declaration:
The following compile-time information is then associated with the method invocation for use at run time:
this (§15.8.3) is not defined.)
static. If the compile-time declaration for the method invocation is for an instance method, then a compile-time error occurs. (The reason is that a method invocation of this form does not specify a reference to an object that can serve as this within the instance method.)
super.NonWildTypeArgumentsopt Identifier, then:
abstract, a compile-time error occurs
super.NonWildTypeArgumentsopt Identifier, then:
abstract, a compile-time error occurs
void, then the method invocation must be a top-level expression, that is, the Expression in an expression statement (§14.8) or in the ForInit or ForUpdate part of a for statement (§14.14), or a compile-time error occurs. (The reason is that such a method invocation produces no value and so must be used only in a situation where a value is not needed.)
If the compile-time declaration for the method invocation is not void.
static modifier, then the invocation mode is static.
private modifier, then the invocation mode is nonvirtual.
super . Identifier or of the form ClassName.super.Identifier then the invocation mode is super.
interface.
virtual.
void, then the type of the method invocation expression is the result type specified in the compile-time declaration.15.12.4 Runtime Evaluation of Method Invocation
At run time, method invocation requires five steps. First, a target reference may be computed. Second, the argument expressions are evaluated. Third, the accessibility of the method to be invoked is checked. Fourth, the actual code for the method to be executed is located. Fifth, a new activation frame is created, synchronization is performed if necessary, and control is transferred to the method code.15.12.4.1 Compute Target Reference (If Necessary)
There are several cases to consider, depending on which of the five productions for MethodInvocation (§15.12) is involved:
static, then there is no target reference.
this. It is a compile-time error if the nth lexically enclosing instance (§8.1.3) of this does not exist.
. Identifier, then there is no target reference.
. Identifier, then there are two subcases:
super, is involved, then the target reference is the value of this.
super, is involved, then the target reference is the value of ClassName.this.
15.12.4.2 Evaluate Arguments
The process of evaluating of the argument list differs, depending on whether the method being invoked is a fixed arity method or a variable arity method (§8.4.1).  0 actual argument expressions.
0 actual argument expressions.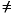 n actual argument expressions, or, if m is being invoked with k=n actual argument expressions and the type of the kth argument expression is not assignment compatible with T[], then the argument list (e1, ... , en-1, en, ...ek) is evaluated as if it were written as (e1, ..., en-1, new T[]{en, ..., ek}).
n actual argument expressions, or, if m is being invoked with k=n actual argument expressions and the type of the kth argument expression is not assignment compatible with T[], then the argument list (e1, ... , en-1, en, ...ek) is evaluated as if it were written as (e1, ..., en-1, new T[]{en, ..., ek}). j
j n. Evaluation then continues, using the argument values, as described below.
n. Evaluation then continues, using the argument values, as described below.15.12.4.3 Check Accessibility of Type and Method
Let C be the class containing the method invocation, and let T be the qualifying type of the method invocation (§13.1), and m be the name of the method, as determined at compile time (§15.12.3). An implementation of the Java programming language must insure, as part of linkage, that the method m still exists in the type T. If this is not true, then a NoSuchMethodError (which is a subclass of IncompatibleClassChangeError) occurs. If the invocation mode is interface, then the implementation must also check that the target reference type still implements the specified interface. If the target reference type does not still implement the interface, then an IncompatibleClassChangeError occurs.
For the method m:public, then T is accessible.
If either T or m is not accessible, then an public, then m is accessible. (All members of interfaces are public (§9.2)).
protected, then m is accessible if and only if either T is in the same package as C, or C is T or a subclass of T.
private, then m is accessible if and only if C is T, or C encloses T, or T encloses C, or T and C are both enclosed by a third class.
IllegalAccessError occurs (§12.3).15.12.4.4 Locate Method to Invoke
The strategy for method lookup depends on the invocation mode.static, no target reference is needed and overriding is not allowed. Method m of class T is the one to be invoked.null, a NullPointerException is thrown at this point. Otherwise, the target reference is said to refer to a target object and will be used as the value of the keyword this in the invoked method. The other four possibilities for the invocation mode are then considered.nonvirtual, overriding is not allowed. Method m of class T is the one to be invoked.interface, virtual, or super, and overriding may occur. A dynamic method lookup is used. The dynamic lookup process starts from a class S, determined as follows:
The dynamic method lookup uses the following procedure to search class S, and then the superclasses of class S, as necessary, for method m.interface or virtual, then S is initially the actual run-time class R of the target object. This is true even if the target object is an array instance. (Note that for invocation mode interface, R necessarily implements T; for invocation mode virtual, R is necessarily either T or a subclass of T.)
super, then S is initially the qualifying type (§13.1) of the method invocation.
super or interface, then this is the method to be invoked, and the procedure terminates.
virtual, and the declaration in S overrides (§8.4.8.1) X.m, then the method declared in S is the method to be invoked, and the procedure terminates.
15.12.4.5 Create Frame, Synchronize, Transfer Control
A method m in some class S has been identified as the one to be invoked.StackOverflowError is thrown.this, if there is a target reference. Before each argument value is assigned to its corresponding parameter variable, it is subjected to method invocation conversion (§5.3), which includes any required value set conversion (§5.1.13).ClassCastException is thrown.
Now, given an invocationclass C<T> { abstract T id(T x); }
class D extends C<String> { String id(String x) { return x; } }
The erasure of the actual method being invoked, C c = new D();
c.id(new Object()); // fails with a ClassCastException
C.id(). The former takes an argument of type String while the latter takes an argument of type Object. The invocation fails with a ClassCastException before the body of the method is executed.D:
This is the method that would actually be invoked by the Java virtual machine in response to the call Object id(Object x) { return id((String) x); }
c.id(new Object()) shown above, and it will execute the cast and fail, as required.
native method but the necessary native, implementation-dependent binary code has not been loaded or otherwise cannot be dynamically linked, then an UnsatisfiedLinkError is thrown.synchronized, control is transferred to the body of the method m to be invoked.synchronized, then an object must be locked before the transfer of control. No further progress can be made until the current thread can obtain the lock. If there is a target reference, then the target must be locked; otherwise the Class object for class S, the class of the method m, must be locked. Control is then transferred to the body of the method m to be invoked. The object is automatically unlocked when execution of the body of the method has completed, whether normally or abruptly. The locking and unlocking behavior is exactly as if the body of the method were embedded in a synchronized statement (§14.19).15.12.4.6 Example: Target Reference and Static Methods
When a target reference is computed and then discarded because the invocation mode is static, the reference is not examined to see whether it is null:
which prints:class Test {
static void mountain() {
System.out.println("Monadnock");
}
static Test favorite(){
System.out.print("Mount ");
return null;
}
public static void main(String[] args) {
favorite().mountain();
}
}
Here Mount Monadnock
favorite returns null, yet no NullPointerException is thrown.15.12.4.7 Example: Evaluation Order
As part of an instance method invocation (§15.12), there is an expression that denotes the object to be invoked. This expression appears to be fully evaluated before any part of any argument expression to the method invocation is evaluated.
the occurrence of class Test {
public static void main(String[] args) {
String s = "one";
if (s.startsWith(s = "two"))
System.out.println("oops");
}
}
s before ".startsWith" is evaluated first, before the argument expression s="two". Therefore, a reference to the string "one" is remembered as the target reference before the local variable s is changed to refer to the string "two". As a result, the startsWith method is invoked for target object "one" with argument "two", so the result of the invocation is false, as the string "one" does not start with "two". It follows that the test program does not print "oops".15.12.4.8 Example: Overriding
In the example:
the subclass class Point {
final int EDGE = 20;
int x, y;
void move(int dx, int dy) {
x += dx; y += dy;
if (Math.abs(x) >= EDGE || Math.abs(y) >= EDGE)
clear();
}
void clear() {
System.out.println("\tPoint clear");
x = 0; y = 0;
}
}
class ColoredPoint extends Point {
int color;
void clear() {
System.out.println("\tColoredPoint clear");
super.clear();
color = 0;
}
}
ColoredPoint extends the clear abstraction defined by its superclass Point. It does so by overriding the clear method with its own method, which invokes the clear method of its superclass, using the form super.clear.clear is a ColoredPoint. Even the method move in Point invokes the clear method of class ColoredPoint when the class of this is ColoredPoint, as shown by the output of this test program:
which is:class Test {
public static void main(String[] args) {
Point p = new Point();
System.out.println("p.move(20,20):");
p.move(20, 20);
ColoredPoint cp = new ColoredPoint();
System.out.println("cp.move(20,20):");
cp.move(20, 20);
p = new ColoredPoint();
System.out.println("p.move(20,20), p colored:");
p.move(20, 20);
}
}
p.move(20,20):
Point clear
cp.move(20,20):
ColoredPoint clear
Point clear
p.move(20,20), p colored:
ColoredPoint clear
Point clear
clear in the body of Point.move (which is really syntactic shorthand for this.clear) invokes a method chosen "late" (at run time, based on the run-time class of the object referenced by this) rather than a method chosen "early" (at compile time, based only on the type of this). This provides the programmer a powerful way of extending abstractions and is a key idea in object-oriented programming.15.12.4.9 Example: Method Invocation using super
An overridden instance method of a superclass may be accessed by using the keyword super to access the members of the immediate superclass, bypassing any overriding declaration in the class that contains the method invocation.super means the same as a cast of this (§15.11.2), but this equivalence does not hold true for method invocation. This is demonstrated by the example:
which produces the output:class T1 {
String s() { return "1"; }
}
class T2 extends T1 {
String s() { return "2"; }
}
class T3 extends T2 {
String s() { return "3"; }
void test() {
System.out.println("s()=\t\t"+s());
System.out.println("super.s()=\t"+super.s());
System.out.print("((T2)this).s()=\t");
System.out.println(((T2)this).s());
System.out.print("((T1)this).s()=\t");
System.out.println(((T1)this).s());
}
}
class Test {
public static void main(String[] args) {
T3 t3 = new T3();
t3.test();
}
}
s()= 3
super.s()= 2
((T2)this).s()= 3
((T1)this).s()= 3
T1 and T2 do not change the method that is invoked, because the instance method to be invoked is chosen according to the run-time class of the object referred to be this. A cast does not change the class of an object; it only checks that the class is compatible with the specified type.15.13 Array Access Expressions
An array access expression refers to a variable that is a component of an array.
An array access expression contains two subexpressions, the array reference expression (before the left bracket) and the index expression (within the brackets). Note that the array reference expression may be a name or any primary expression that is not an array creation expression (§15.10).
ArrayAccess:
ExpressionName [ Expression ]
PrimaryNoNewArray [ Expression ]
int.final, even if the array reference was obtained from a final variable.15.13.1 Runtime Evaluation of Array Access
An array access expression is evaluated using the following procedure:
null, then a NullPointerException is thrown.
ArrayIndexOutOfBoundsException is thrown.
final, even if the array reference expression is a final variable.)
15.13.2 Examples: Array Access Evaluation Order
In an array access, the expression to the left of the brackets appears to be fully evaluated before any part of the expression within the brackets is evaluated. For example, in the (admittedly monstrous) expression a[(a=b)[3]], the expression a is fully evaluated before the expression (a=b)[3]; this means that the original value of a is fetched and remembered while the expression (a=b)[3] is evaluated. This array referenced by the original value of a is then subscripted by a value that is element 3 of another array (possibly the same array) that was referenced by b and is now also referenced by a.
prints:class Test {
public static void main(String[] args) {
int[] a = { 11, 12, 13, 14 };
int[] b = { 0, 1, 2, 3 };
System.out.println(a[(a=b)[3]]);
}
}
because the monstrous expression's value is equivalent to 14
a[b[3]] or a[3] or 14.
prints: class Test {
public static void main(String[] args) {
int index = 1;
try {
skedaddle()[index=2]++;
} catch (Exception e) {
System.out.println(e + ", index=" + index);
}
}
static int[] skedaddle() throws Exception {
throw new Exception("Ciao");
}
}
because the embedded assignment of java.lang.Exception: Ciao, index=1
2 to index never occurs.null instead of a reference to an array, then a NullPointerException is thrown at run time, but only after all parts of the array access expression have been evaluated and only if these evaluations completed normally. Thus, the example:
prints:class Test {
public static void main(String[] args) {
int index = 1;
try {
nada()[index=2]++;
} catch (Exception e) {
System.out.println(e + ", index=" + index);
}
}
static int[] nada() { return null; }
}
because the embedded assignment of java.lang.NullPointerException, index=2
2 to index occurs before the check for a null pointer. As a related example, the program:
always prints:class Test {
public static void main(String[] args) {
int[] a = null;
try {
int i = a[vamoose()];
System.out.println(i);
} catch (Exception e) {
System.out.println(e);
}
}
static int vamoose() throws Exception {
throw new Exception("Twenty-three skidoo!");
}
}
java.lang.Exception: Twenty-three skidoo!
NullPointerException never occurs, because the index expression must be completely evaluated before any part of the indexing operation occurs, and that includes the check as to whether the value of the left-hand operand is null.15.14 Postfix Expressions
Postfix expressions include uses of the postfix ++ and -- operators. Also, as discussed in §15.8, names are not considered to be primary expressions, but are handled separately in the grammar to avoid certain ambiguities. They become interchangeable only here, at the level of precedence of postfix expressions.
PostfixExpression:
Primary
ExpressionName
PostIncrementExpression
PostDecrementExpression
15.14.1 Expression Names
The rules for evaluating expression names are given in §6.5.6. 15.14.2 Postfix Increment Operator ++
A postfix expression followed by a
PostIncrementExpression:
PostfixExpression ++
++ operator is a postfix increment expression. The result of the postfix expression must be a variable of a type that is convertible (§5.1.8) to a numeric type, or a compile-time error occurs. The type of the postfix increment expression is the type of the variable. The result of the postfix increment expression is not a variable, but a value.1 is added to the value of the variable and the sum is stored back into the variable. Before the addition, binary numeric promotion (§5.6.2) is performed on the value 1 and the value of the variable. If necessary, the sum is narrowed by a narrowing primitive conversion (§5.1.3) and/or subjected to boxing conversion (§5.1.7) to the type of the variable before it is stored. The value of the postfix increment expression is the value of the variable before the new value is stored.final cannot be incremented (unless it is a definitely unassigned (§16) blank final variable (§4.12.4)), because when an access of such a final variable is used as an expression, the result is a value, not a variable. Thus, it cannot be used as the operand of a postfix increment operator.15.14.3 Postfix Decrement Operator --
A postfix expression followed by a
PostDecrementExpression:
PostfixExpression --
-- operator is a postfix decrement expression. The result of the postfix expression must be a variable of a type that is convertible (§5.1.8) to a numeric type, or a compile-time error occurs. The type of the postfix decrement expression is the type of the variable. The result of the postfix decrement expression is not a variable, but a value.1 is subtracted from the value of the variable and the difference is stored back into the variable. Before the subtraction, binary numeric promotion (§5.6.2) is performed on the value 1 and the value of the variable. If necessary, the difference is narrowed by a narrowing primitive conversion (§5.1.3) and/or subjected to boxing conversion (§5.1.7) to the type of the variable before it is stored. The value of the postfix decrement expression is the value of the variable before the new value is stored.final cannot be decremented (unless it is a definitely unassigned (§16) blank final variable (§4.12.4)), because when an access of such a final variable is used as an expression, the result is a value, not a variable. Thus, it cannot be used as the operand of a postfix decrement operator.15.15 Unary Operators
The unary operators include +, -, ++, --, ~, !, and cast operators. Expressions with unary operators group right-to-left, so that -~x means the same as -(~x).
The following productions from §15.16 are repeated here for convenience:
UnaryExpression:
PreIncrementExpression
PreDecrementExpression
+ UnaryExpression
- UnaryExpression
UnaryExpressionNotPlusMinus
PreIncrementExpression:
++ UnaryExpression
PreDecrementExpression:
-- UnaryExpression
UnaryExpressionNotPlusMinus:
PostfixExpression
~ UnaryExpression
! UnaryExpression
CastExpression
CastExpression:
( PrimitiveType ) UnaryExpression
( ReferenceType ) UnaryExpressionNotPlusMinus
15.15.1 Prefix Increment Operator ++
A unary expression preceded by a ++ operator is a prefix increment expression. The result of the unary expression must be a variable of a type that is convertible (§5.1.8) to a numeric type, or a compile-time error occurs. The type of the prefix increment expression is the type of the variable. The result of the prefix increment expression is not a variable, but a value.1 is added to the value of the variable and the sum is stored back into the variable. Before the addition, binary numeric promotion (§5.6.2) is performed on the value 1 and the value of the variable. If necessary, the sum is narrowed by a narrowing primitive conversion (§5.1.3) and/or subjected to boxing conversion (§5.1.7) to the type of the variable before it is stored. The value of the prefix increment expression is the value of the variable after the new value is stored.final cannot be incremented (unless it is a definitely unassigned (§16) blank final variable (§4.12.4)), because when an access of such a final variable is used as an expression, the result is a value, not a variable. Thus, it cannot be used as the operand of a prefix increment operator.15.15.2 Prefix Decrement Operator --
A unary expression preceded by a -- operator is a prefix decrement expression. The result of the unary expression must be a variable of a type that is convertible (§5.1.8) to a numeric type, or a compile-time error occurs. The type of the prefix decrement expression is the type of the variable. The result of the prefix decrement expression is not a variable, but a value.1 is subtracted from the value of the variable and the difference is stored back into the variable. Before the subtraction, binary numeric promotion (§5.6.2) is performed on the value 1 and the value of the variable. If necessary, the difference is narrowed by a narrowing primitive conversion (§5.1.3) and/or subjected to boxing conversion (§5.1.7) to the type of the variable before it is stored. The value of the prefix decrement expression is the value of the variable after the new value is stored.final cannot be decremented (unless it is a definitely unassigned (§16) blank final variable (§4.12.4)), because when an access of such a final variable is used as an expression, the result is a value, not a variable. Thus, it cannot be used as the operand of a prefix decrement operator.15.15.3 Unary Plus Operator +
The type of the operand expression of the unary + operator must be a type that is convertible (§5.1.8) to a primitive numeric type, or a compile-time error occurs. Unary numeric promotion (§) is performed on the operand. The type of the unary plus expression is the promoted type of the operand. The result of the unary plus expression is not a variable, but a value, even if the result of the operand expression is a variable.15.15.4 Unary Minus Operator -
The type of the operand expression of the unary - operator must be a type that is convertible (§5.1.8) to a primitive numeric type, or a compile-time error occurs. Unary numeric promotion (§) is performed on the operand. The type of the unary minus expression is the promoted type of the operand.int or long results in that same maximum negative number. Overflow occurs in this case, but no exception is thrown. For all integer values x, -x equals (~x)+1.x is +0.0, then 0.0-x is +0.0, but -x is -0.0. Unary minus merely inverts the sign of a floating-point number. Special cases of interest:
15.15.5 Bitwise Complement Operator ~
The type of the operand expression of the unary ~ operator must be a type that is convertible (§5.1.8) to a primitive integral type, or a compile-time error occurs. Unary numeric promotion (§) is performed on the operand. The type of the unary bitwise complement expression is the promoted type of the operand.~x equals (-x)-1.15.15.6 Logical Complement Operator !
The type of the operand expression of the unary ! operator must be boolean or Boolean, or a compile-time error occurs. The type of the unary logical complement expression is boolean.true if the (possibly converted) operand value is false and false if the (possibly converted) operand value is true.15.16 Cast Expressions
A cast expression converts, at run time, a value of one numeric type to a similar value of another numeric type; or confirms, at compile time, that the type of an expression is boolean; or checks, at run time, that a reference value refers to an object whose class is compatible with a specified reference type.
CastExpression:
( PrimitiveType Dimsopt ) UnaryExpression
( ReferenceType ) UnaryExpressionNotPlusMinus
float or type double. Consequently, a cast to type float within an expression that is not FP-strict (§15.4) does not necessarily cause its value to be converted to an element of the float value set, and a cast to type double within an expression that is not FP-strict does not necessarily cause its value to be converted to an element of the double value set.ClassCastException is thrown if a cast is found at run time to be impermissible.15.17 Multiplicative Operators
The operators *, /, and % are called the multiplicative operators. They have the same precedence and are syntactically left-associative (they group left-to-right).
The type of each of the operands of a multiplicative operator must be a type that is convertible (§5.1.8) to a primitive numeric type, or a compile-time error occurs. Binary numeric promotion is performed on the operands (§5.6.2). The type of a multiplicative expression is the promoted type of its operands. If this promoted type is
MultiplicativeExpression:
UnaryExpression
MultiplicativeExpression * UnaryExpression
MultiplicativeExpression / UnaryExpression
MultiplicativeExpression % UnaryExpression
int or long, then integer arithmetic is performed; if this promoted type is float or double, then floating-point arithmetic is performed.15.17.1 Multiplication Operator *
The binary * operator performs multiplication, producing the product of its operands. Multiplication is a commutative operation if the operand expressions have no side effects. While integer multiplication is associative when the operands are all of the same type, floating-point multiplication is not associative.
float, then the float value set must be chosen.
double, then the double value set must be chosen.
float, then either the float value set or the float-extended-exponent value set may be chosen, at the whim of the implementation.
double, then either the double value set or the double-extended-exponent value set may be chosen, at the whim of the implementation.
Despite the fact that overflow, underflow, or loss of information may occur, evaluation of a multiplication operator * never throws a run-time exception.15.17.2 Division Operator /
The binary / operator performs division, producing the quotient of its operands. The left-hand operand is the dividend and the right-hand operand is the divisor.0. That is, the quotient produced for operands n and d that are integers after binary numeric promotion (§5.6.2) is an integer value q whose magnitude is as large as possible while satisfying |d·q| |n|; moreover, q is positive when |n|
|n|; moreover, q is positive when |n|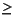 |d| and n and d have the same sign, but q is negative when |n|
|d| and n and d have the same sign, but q is negative when |n|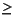 |d| and n and d have opposite signs. There is one special case that does not satisfy this rule: if the dividend is the negative integer of largest possible magnitude for its type, and the divisor is
|d| and n and d have opposite signs. There is one special case that does not satisfy this rule: if the dividend is the negative integer of largest possible magnitude for its type, and the divisor is -1, then integer overflow occurs and the result is equal to the dividend. Despite the overflow, no exception is thrown in this case. On the other hand, if the value of the divisor in an integer division is 0, then an ArithmeticException is thrown.
float, then the float value set must be chosen.
double, then the double value set must be chosen.
float, then either the float value set or the float-extended-exponent value set may be chosen, at the whim of the implementation.
double, then either the double value set or the double-extended-exponent value set may be chosen, at the whim of the implementation.
Despite the fact that overflow, underflow, division by zero, or loss of information may occur, evaluation of a floating-point division operator / never throws a run-time exception15.17.3 Remainder Operator %
The binary % operator is said to yield the remainder of its operands from an implied division; the left-hand operand is the dividend and the right-hand operand is the divisor.(a/b)*b+(a%b) is equal to a. This identity holds even in the special case that the dividend is the negative integer of largest possible magnitude for its type and the divisor is -1 (the remainder is 0). It follows from this rule that the result of the remainder operation can be negative only if the dividend is negative, and can be positive only if the dividend is positive; moreover, the magnitude of the result is always less than the magnitude of the divisor. If the value of the divisor for an integer remainder operator is 0, then an ArithmeticException is thrown.Examples:
The result of a floating-point remainder operation as computed by the 5%3 produces 2 (note that 5/3 produces 1)
5%(-3) produces 2 (note that 5/(-3) produces -1)
(-5)%3 produces -2 (note that (-5)/3 produces -1)
(-5)%(-3) produces -2 (note that (-5)/(-3) produces 1)
% operator is not the same as that produced by the remainder operation defined by IEEE 754. The IEEE 754 remainder operation computes the remainder from a rounding division, not a truncating division, and so its behavior is not analogous to that of the usual integer remainder operator. Instead, the Java programming language defines % on floating-point operations to behave in a manner analogous to that of the integer remainder operator; this may be compared with the C library function fmod. The IEEE 754 remainder operation may be computed by the library routine Math.IEEEremainder.
Evaluation of a floating-point remainder operator % never throws a run-time exception, even if the right-hand operand is zero. Overflow, underflow, or loss of precision cannot occur.5.0%3.0 produces 2.0
5.0%(-3.0) produces 2.0
(-5.0)%3.0 produces -2.0
(-5.0)%(-3.0) produces -2.0
15.18 Additive Operators
The operators + and - are called the additive operators. They have the same precedence and are syntactically left-associative (they group left-to-right).
If the type of either operand of a + operator is
AdditiveExpression:
MultiplicativeExpression
AdditiveExpression + MultiplicativeExpression
AdditiveExpression - MultiplicativeExpression
String, then the operation is string concatenation.+ operator must be a type that is convertible (§5.1.8) to a primitive numeric type, or a compile-time error occurs. - operator must be a type that is convertible (§5.1.8) to a primitive numeric type, or a compile-time error occurs. 15.18.1 String Concatenation Operator +
If only one operand expression is of type String, then string conversion is performed on the other operand to produce a string at run time. The result is a reference to a String object (newly created, unless the expression is a compile-time constant expression (§15.28))that is the concatenation of the two operand strings. The characters of the left-hand operand precede the characters of the right-hand operand in the newly created string. If an operand of type String is null, then the string "null" is used instead of that operand.15.18.1.1 String Conversion
Any type may be converted to type String by string conversion.
This reference value is then converted to type boolean, then use new Boolean(x).
char, then use new Character(x).
byte, short, or int, then use new Integer(x).
long, then use new Long(x).
float, then use new Float(x).
double, then use new Double(x).
String by string conversion.null, it is converted to the string "null" (four ASCII characters n, u, l, l). Otherwise, the conversion is performed as if by an invocation of the toString method of the referenced object with no arguments; but if the result of invoking the toString method is null, then the string "null" is used instead. toString method is defined by the primordial class Object; many classes override it, notably Boolean, Character, Integer, Long, Float, Double, and String.15.18.1.2 Optimization of String Concatenation
An implementation may choose to perform conversion and concatenation in one step to avoid creating and then discarding an intermediate String object. To increase the performance of repeated string concatenation, a Java compiler may use the StringBuffer class or a similar technique to reduce the number of intermediate String objects that are created by evaluation of an expression.15.18.1.3 Examples of String Concatenation
The example expression:
produces the result:"The square root of 2 is " + Math.sqrt(2)
"The square root of 2 is 1.4142135623730952"
is always regarded as meaning:
a + b + c
Therefore the result of the expression:(a + b) + c
is:1 + 2 + " fiddlers"
but the result of:"3 fiddlers"
is:"fiddlers " + 1 + 2
"fiddlers 12"
class Bottles {
static void printSong(Object stuff, int n) {
String plural = (n == 1) ? "" : "s";
loop: while (true) {
System.out.println(n + " bottle" + plural
+ " of " + stuff + " on the wall,");
System.out.println(n + " bottle" + plural
+ " of " + stuff + ";");
System.out.println("You take one down "
+ "and pass it around:");
--n;
plural = (n == 1) ? "" : "s";
if (n == 0)
break loop;
System.out.println(n + " bottle" + plural
+ " of " + stuff + " on the wall!");
System.out.println();
}
System.out.println("No bottles of " +
stuff + " on the wall!");
}
}
printSong will print a version of a children's song. Popular values for stuff include "pop" and "beer"; the most popular value for n is 100. Here is the output that results from Bottles.printSong("slime", 3):3 bottles of slime on the wall,
3 bottles of slime;
You take one down and pass it around:
2 bottles of slime on the wall!
2 bottles of slime on the wall,
2 bottles of slime;
You take one down and pass it around:
1 bottle of slime on the wall!
1 bottle of slime on the wall,
1 bottle of slime;
You take one down and pass it around:
No bottles of slime on the wall!
bottle" when appropriate rather than the plural "bottles"; note also how the string concatenation operator was used to break the long constant string:"You take one down and pass it around:"
15.18.2 Additive Operators (+ and -) for Numeric Types
The binary + operator performs addition when applied to two operands of numeric type, producing the sum of the operands. The binary - operator performs subtraction, producing the difference of two numeric operands.int or long, then integer arithmetic is performed; if this promoted type is float or double, then floating-point arithmetic is performed.
float, then the float value set must be chosen.
double, then the double value set must be chosen.
float, then either the float value set or the float-extended-exponent value set may be chosen, at the whim of the implementation.
double, then either the double value set or the double-extended-exponent value set may be chosen, at the whim of the implementation.
The binary - operator performs subtraction when applied to two operands of numeric type producing the difference of its operands; the left-hand operand is the minuend and the right-hand operand is the subtrahend. For both integer and floating-point subtraction, it is always the case that a-b produces the same result as a+(-b). x is +0.0, then 0.0-x is +0.0, but -x is -0.0. 15.19 Shift Operators
The shift operators include left shift <<, signed right shift >>, and unsigned right shift >>>; they are syntactically left-associative (they group left-to-right). The left-hand operand of a shift operator is the value to be shifted; the right-hand operand specifies the shift distance.
The type of each of the operands of a shift operator must be a type that is convertible (§5.1.8) to a primitive integral type, or a compile-time error occurs. Binary numeric promotion (§5.6.2) is not performed on the operands; rather, unary numeric promotion (§) is performed on each operand separately. The type of the shift expression is the promoted type of the left-hand operand.
ShiftExpression:
AdditiveExpression
ShiftExpression << AdditiveExpression
ShiftExpression >> AdditiveExpression
ShiftExpression >>> AdditiveExpression
int, only the five lowest-order bits of the right-hand operand are used as the shift distance. It is as if the right-hand operand were subjected to a bitwise logical AND operator & (§15.22.1) with the mask value 0x1f. The shift distance actually used is therefore always in the range 0 to 31, inclusive.long, then only the six lowest-order bits of the right-hand operand are used as the shift distance. It is as if the right-hand operand were subjected to a bitwise logical AND operator & (§15.22.1) with the mask value 0x3f. The shift distance actually used is therefore always in the range 0 to 63, inclusive.n<<s is n left-shifted s bit positions; this is equivalent (even if overflow occurs) to multiplication by two to the power s.n>>s is n right-shifted s bit positions with sign-extension. The resulting value is n/s. For nonnegative values of n, this is equivalent to truncating integer division, as computed by the integer division operator /, by two to the power s.n>>>s is n right-shifted s bit positions with zero-extension. If n is positive, then the result is the same as that of n>>s; if n is negative, the result is equal to that of the expression (n>>s)+(2<<~s) if the type of the left-hand operand is int, and to the result of the expression (n>>s)+(2L<<~s) if the type of the left-hand operand is long. The added term (2<<~s) or (2L<<~s) cancels out the propagated sign bit. (Note that, because of the implicit masking of the right-hand operand of a shift operator, ~s as a shift distance is equivalent to 31-s when shifting an int value and to 63-s when shifting a long value.)15.20 Relational Operators
The relational operators are syntactically left-associative (they group left-to-right), but this fact is not useful; for example, a<b<c parses as (a<b)<c, which is always a compile-time error, because the type of a<b is always boolean and < is not an operator on boolean values.
The type of a relational expression is always
RelationalExpression:
ShiftExpression
RelationalExpression < ShiftExpression
RelationalExpression > ShiftExpression
RelationalExpression <= ShiftExpression
RelationalExpression >= ShiftExpression
RelationalExpression instanceof ReferenceType
boolean.15.20.1 Numerical Comparison Operators <, <=, >, and >=
The type of each of the operands of a numerical comparison operator must be a type that is convertible (§5.1.8) to a primitive numeric type, or a compile-time error occurs. Binary numeric promotion is performed on the operands (§5.6.2). If the promoted type of the operands is int or long, then signed integer comparison is performed; if this promoted type is float or double, then floating-point comparison is performed.
Subject to these considerations for floating-point numbers, the following rules then hold for integer operands or for floating-point operands other than NaN:false.
-0.0<0.0 is false, for example, but -0.0<=0.0 is true. (Note, however, that the methods Math.min and Math.max treat negative zero as being strictly smaller than positive zero.)
< operator is true if the value of the left-hand operand is less than the value of the right-hand operand, and otherwise is false.
<= operator is true if the value of the left-hand operand is less than or equal to the value of the right-hand operand, and otherwise is false.
> operator is true if the value of the left-hand operand is greater than the value of the right-hand operand, and otherwise is false.
>= operator is true if the value of the left-hand operand is greater than or equal to the value of the right-hand operand, and otherwise is false.
15.20.2 Type Comparison Operator instanceof
The type of a RelationalExpression operand of the instanceof operator must be a reference type or the null type; otherwise, a compile-time error occurs. The ReferenceType mentioned after the instanceof operator must denote a reference type; otherwise, a compile-time error occurs. It is a compile-time error if the ReferenceType mentioned after the instanceof operator does not denote a reifiable type (§4.7).instanceof operator is true if the value of the RelationalExpression is not null and the reference could be cast (§15.16) to the ReferenceType without raising a ClassCastException. Otherwise the result is false.instanceof relational expression likewise produces a compile-time error. In such a situation, the result of the instanceof expression could never be true.
This example results in two compile-time errors. The cast class Point { int x, y; }
class Element { int atomicNumber; }
class Test {
public static void main(String[] args) {
Point p = new Point();
Element e = new Element();
if (e instanceof Point) { // compile-time error
System.out.println("I get your point!");
p = (Point)e; // compile-time error
}
}
}
(Point)e is incorrect because no instance of Element or any of its possible subclasses (none are shown here) could possibly be an instance of any subclass of Point. The instanceof expression is incorrect for exactly the same reason. If, on the other hand, the class Point were a subclass of Element (an admittedly strange notion in this example):
then the cast would be possible, though it would require a run-time check, and the class Point extends Element { int x, y; }
instanceof expression would then be sensible and valid. The cast (Point)e would never raise an exception because it would not be executed if the value of e could not correctly be cast to type Point.
15.21 Equality Operators
The equality operators are syntactically left-associative (they group left-to-right), but this fact is essentially never useful; for example, a==b==c parses as (a==b)==c. The result type of a==b is always boolean, and c must therefore be of type boolean or a compile-time error occurs. Thus, a==b==c does not test to see whether a, b, and c are all equal.
The == (equal to) and the!= (not equal to) operators are analogous to the relational operators except for their lower precedence. Thus,
EqualityExpression:
RelationalExpression
EqualityExpression == RelationalExpression
EqualityExpression != RelationalExpression
a<b==c<d is true whenever a<b and c<d have the same truth value.boolean or Boolean, or two operands that are each of either reference type or the null type. All other cases result in a compile-time error. The type of an equality expression is always boolean.a!=b produces the same result as !(a==b). The equality operators are commutative if the operand expressions have no side effects.15.21.1 Numerical Equality Operators == and !=
If the operands of an equality operator are both of numeric type, or one is of numeric type and the other is convertible (§5.1.8) to numeric type, binary numeric promotion is performed on the operands (§5.6.2). If the promoted type of the operands is int or long, then an integer equality test is performed; if the promoted type is float or double, then a floating-point equality test is performed.
Subject to these considerations for floating-point numbers, the following rules then hold for integer operands or for floating-point operands other than NaN:== is false but the result of != is true. Indeed, the test x!=x is true if and only if the value of x is NaN. (The methods Float.isNaN and Double.isNaN may also be used to test whether a value is NaN.)
-0.0==0.0 is true, for example.
== operator is true if the value of the left-hand operand is equal to the value of the right-hand operand; otherwise, the result is false.
!= operator is true if the value of the left-hand operand is not equal to the value of the right-hand operand; otherwise, the result is false.
15.21.2 Boolean Equality Operators == and !=
If the operands of an equality operator are both of type boolean, or if one operand is of type boolean and the other is of type Boolean, then the operation is boolean equality. The boolean equality operators are associative. Boolean it is subjected to unboxing conversion (§5.1.8).== is true if the operands (after any required unboxing conversion) are both true or both false; otherwise, the result is false.!= is false if the operands are both true or both false; otherwise, the result is true. Thus != behaves the same as ^ (§15.22.2) when applied to boolean operands.15.21.3 Reference Equality Operators == and !=
If the operands of an equality operator are both of either reference type or the null type, then the operation is object equality.== is true if the operand values are both null or both refer to the same object or array; otherwise, the result is false.!= is false if the operand values are both null or both refer to the same object or array; otherwise, the result is true.== may be used to compare references of type String, such an equality test determines whether or not the two operands refer to the same String object. The result is false if the operands are distinct String objects, even if they contain the same sequence of characters. The contents of two strings s and t can be tested for equality by the method invocation s.equals(t). See also §3.10.5.15.22 Bitwise and Logical Operators
The bitwise operators and logical operators include the AND operator &, exclusive OR operator ^, and inclusive OR operator |. These operators have different precedence, with & having the highest precedence and | the lowest precedence. Each of these operators is syntactically left-associative (each groups left-to-right). Each operator is commutative if the operand expressions have no side effects. Each operator is associative.
The bitwise and logical operators may be used to compare two operands of numeric type or two operands of type
AndExpression:
EqualityExpression
AndExpression & EqualityExpression
ExclusiveOrExpression:
AndExpression
ExclusiveOrExpression ^ AndExpression
InclusiveOrExpression:
ExclusiveOrExpression
InclusiveOrExpression | ExclusiveOrExpression
boolean. All other cases result in a compile-time error.15.22.1 Integer Bitwise Operators &, ^, and |
When both operands of an operator &, ^, or | are of a type that is convertible (§5.1.8) to a primitive integral type, binary numeric promotion is first performed on the operands (§5.6.2). The type of the bitwise operator expression is the promoted type of the operands.&, the result value is the bitwise AND of the operand values.^, the result value is the bitwise exclusive OR of the operand values.|, the result value is the bitwise inclusive OR of the operand values.0xff00 & 0xf0f0 is 0xf000. The result of 0xff00 ^ 0xf0f0 is 0x0ff0.The result of 0xff00 | 0xf0f0 is 0xfff0.15.22.2 Boolean Logical Operators &, ^, and |
When both operands of a &, ^, or | operator are of type boolean or Boolean, then the type of the bitwise operator expression is boolean. In all cases, the operands are subject to unboxing conversion (§5.1.8) as necessary.&, the result value is true if both operand values are true; otherwise, the result is false.^, the result value is true if the operand values are different; otherwise, the result is false.|, the result value is false if both operand values are false; otherwise, the result is true.15.23 Conditional-And Operator &&
The && operator is like & (§15.22.2), but evaluates its right-hand operand only if the value of its left-hand operand is true. It is syntactically left-associative (it groups left-to-right). It is fully associative with respect to both side effects and result value; that is, for any expressions a, b, and c, evaluation of the expression ((a)&&(b))&&(c) produces the same result, with the same side effects occurring in the same order, as evaluation of the expression (a)&&((b)&&(c)).
Each operand of
ConditionalAndExpression:
InclusiveOrExpression
ConditionalAndExpression && InclusiveOrExpression
&& must be of type boolean or Boolean, or a compile-time error occurs. The type of a conditional-and expression is always boolean.Boolean, it is subjected to unboxing conversion (§5.1.8); if the resulting value is false, the value of the conditional-and expression is false and the right-hand operand expression is not evaluated. If the value of the left-hand operand is true, then the right-hand expression is evaluated; if the result has type Boolean, it is subjected to unboxing conversion (§5.1.8); the resulting value becomes the value of the conditional-and expression. Thus, && computes the same result as & on boolean operands. It differs only in that the right-hand operand expression is evaluated conditionally rather than always.15.24 Conditional-Or Operator ||
The || operator is like | (§15.22.2), but evaluates its right-hand operand only if the value of its left-hand operand is false. It is syntactically left-associative (it groups left-to-right). It is fully associative with respect to both side effects and result value; that is, for any expressions a, b, and c, evaluation of the expression ((a)||(b))||(c) produces the same result, with the same side effects occurring in the same order, as evaluation of the expression (a)||((b)||(c)).
Each operand of
ConditionalOrExpression:
ConditionalAndExpression
ConditionalOrExpression || ConditionalAndExpression
|| must be of type boolean or Boolean, or a compile-time error occurs. The type of a conditional-or expression is always boolean.Boolean, it is subjected to unboxing conversion (§5.1.8); if the resulting value is true, the value of the conditional-or expression is true and the right-hand operand expression is not evaluated. If the value of the left-hand operand is false, then the right-hand expression is evaluated; if the result has type Boolean, it is subjected to unboxing conversion (§5.1.8); the resulting value becomes the value of the conditional-or expression. || computes the same result as | on boolean or Boolean operands. It differs only in that the right-hand operand expression is evaluated conditionally rather than always.15.25 Conditional Operator ? :
The conditional operator ? : uses the boolean value of one expression to decide which of two other expressions should be evaluated.a?b:c?d:e?f:g means the same as a?b:(c?d:(e?f:g)).
The conditional operator has three operand expressions;
ConditionalExpression:
ConditionalOrExpression
ConditionalOrExpression ? Expression : ConditionalExpression
? appears between the first and second expressions, and : appears between the second and third expressions.boolean or Boolean, or a compile-time error occurs.void method. In fact, it is not permitted for a conditional expression to appear in any context where an invocation of a void method could appear (§14.8).
At run time, the first operand expression of the conditional expression is evaluated first; if necessary, unboxing conversion is performed on the result; the resulting boolean and the type of the other is of type Boolean, then the type of the conditional expression is boolean.
byte or Byte and the other is of type short or Short, then the type of the conditional expression is short.
byte, short, or char, and the other operand is a constant expression of type int whose value is representable in type T, then the type of the conditional expression is T.
Byte and the other operand is a constant expression of type int whose value is representable in type byte, then the type of the conditional expression is byte.
Short and the other operand is a constant expression of type int whose value is representable in type short, then the type of the conditional expression is short.
Character and the other operand is a constant expression of type int whose value is representable in type char, then the type of the conditional expression is char.
boolean value is then used to choose either the second or the third operand expression:
The chosen operand expression is then evaluated and the resulting value is converted to the type of the conditional expression as determined by the rules stated above. This conversion may include boxing (§5.1.7) or unboxing conversion. The operand expression not chosen is not evaluated for that particular evaluation of the conditional expression. true, then the second operand expression is chosen.
false, then the third operand expression is chosen.
15.26 Assignment Operators
There are 12 assignment operators; all are syntactically right-associative (they group right-to-left). Thus, a=b=c means a=(b=c), which assigns the value of c to b and then assigns the value of b to a.
The result of the first operand of an assignment operator must be a variable, or a compile-time error occurs. This operand may be a named variable, such as a local variable or a field of the current object or class, or it may be a computed variable, as can result from a field access (§15.11) or an array access (§15.13). The type of the assignment expression is the type of the variable after capture conversion (§5.1.10).
AssignmentExpression:
ConditionalExpression
Assignment
Assignment:
LeftHandSide AssignmentOperator AssignmentExpression
LeftHandSide:
ExpressionName
FieldAccess
ArrayAccess
AssignmentOperator: one of
= *= /= %= += -= <<= >>= >>>= &= ^= |=
final cannot be assigned to (unless it is a definitely unassigned (§16) blank final variable (§4.12.4)), because when an access of such a final variable is used as an expression, the result is a value, not a variable, and so it cannot be used as the first operand of an assignment operator. 15.26.1 Simple Assignment Operator =
A compile-time error occurs if the type of the right-hand operand cannot be converted to the type of the variable by assignment conversion (§5.2).
static and the result of the evaluation of e above is null, then a NullPointerException is thrown.
null, then no assignment occurs and a NullPointerException is thrown.
ArrayIndexOutOfBoundsException is thrown.
final). But if the compiler cannot prove at compile time that the array component will be of type TC exactly, then a check must be performed at run time to ensure that the class RC is assignment compatible (§5.2) with the actual type SC of the array component. This check is similar to a narrowing cast (§5.5, §15.16), except that if the check fails, an ArrayStoreException is thrown rather than a ClassCastException. Therefore:
ArrayStoreException is thrown.
This program prints:
class ArrayReferenceThrow extends RuntimeException { }
class IndexThrow extends RuntimeException { }
class RightHandSideThrow extends RuntimeException { }
class IllustrateSimpleArrayAssignment {
static Object[] objects = { new Object(), new Object() };
static Thread[] threads = { new Thread(), new Thread() };
static Object[] arrayThrow() {
throw new ArrayReferenceThrow();
}
static int indexThrow() { throw new IndexThrow(); }
static Thread rightThrow() {
throw new RightHandSideThrow();
}
static String name(Object q) {
String sq = q.getClass().getName();
int k = sq.lastIndexOf('.');
return (k < 0) ? sq : sq.substring(k+1);
}
static void testFour(Object[] x, int j, Object y) {
String sx = x == null ? "null" : name(x[0]) + "s";
String sy = name(y);
System.out.println();
try {
System.out.print(sx + "[throw]=throw => ");
x[indexThrow()] = rightThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print(sx + "[throw]=" + sy + " => ");
x[indexThrow()] = y;
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print(sx + "[" + j + "]=throw => ");
x[j] = rightThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print(sx + "[" + j + "]=" + sy + " => ");
x[j] = y;
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
}
public static void main(String[] args) {
try {
System.out.print("throw[throw]=throw => ");
arrayThrow()[indexThrow()] = rightThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print("throw[throw]=Thread => ");
arrayThrow()[indexThrow()] = new Thread();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print("throw[1]=throw => ");
arrayThrow()[1] = rightThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print("throw[1]=Thread => ");
arrayThrow()[1] = new Thread();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
testFour(null, 1, new StringBuffer());
testFour(null, 1, new StringBuffer());
testFour(null, 9, new Thread());
testFour(null, 9, new Thread());
testFour(objects, 1, new StringBuffer());
testFour(objects, 1, new Thread());
testFour(objects, 9, new StringBuffer());
testFour(objects, 9, new Thread());
testFour(threads, 1, new StringBuffer());
testFour(threads, 1, new Thread());
testFour(threads, 9, new StringBuffer());
testFour(threads, 9, new Thread());
}
}
The most interesting case of the lot is the one thirteenth from the end:throw[throw]=throw => ArrayReferenceThrow
throw[throw]=Thread => ArrayReferenceThrow
throw[1]=throw => ArrayReferenceThrow
throw[1]=Thread => ArrayReferenceThrow
null[throw]=throw => IndexThrow
null[throw]=StringBuffer => IndexThrow
null[1]=throw => RightHandSideThrow
null[1]=StringBuffer => NullPointerException
null[throw]=throw => IndexThrow
null[throw]=StringBuffer => IndexThrow
null[1]=throw => RightHandSideThrow
null[1]=StringBuffer => NullPointerException
null[throw]=throw => IndexThrow
null[throw]=Thread => IndexThrow
null[9]=throw => RightHandSideThrow
null[9]=Thread => NullPointerException
null[throw]=throw => IndexThrow
null[throw]=Thread => IndexThrow
null[9]=throw => RightHandSideThrow
null[9]=Thread => NullPointerException
Objects[throw]=throw => IndexThrow
Objects[throw]=StringBuffer => IndexThrow
Objects[1]=throw => RightHandSideThrow
Objects[1]=StringBuffer => Okay!
Objects[throw]=throw => IndexThrow
Objects[throw]=Thread => IndexThrow
Objects[1]=throw => RightHandSideThrow
Objects[1]=Thread => Okay!
Objects[throw]=throw => IndexThrow
Objects[throw]=StringBuffer => IndexThrow
Objects[9]=throw => RightHandSideThrow
Objects[9]=StringBuffer => ArrayIndexOutOfBoundsException
Objects[throw]=throw => IndexThrow
Objects[throw]=Thread => IndexThrow
Objects[9]=throw => RightHandSideThrow
Objects[9]=Thread => ArrayIndexOutOfBoundsException
Threads[throw]=throw => IndexThrow
Threads[throw]=StringBuffer => IndexThrow
Threads[1]=throw => RightHandSideThrow
Threads[1]=StringBuffer => ArrayStoreException
Threads[throw]=throw => IndexThrow
Threads[throw]=Thread => IndexThrow
Threads[1]=throw => RightHandSideThrow
Threads[1]=Thread => Okay!
Threads[throw]=throw => IndexThrow
Threads[throw]=StringBuffer => IndexThrow
Threads[9]=throw => RightHandSideThrow
Threads[9]=StringBuffer => ArrayIndexOutOfBoundsException
Threads[throw]=throw => IndexThrow
Threads[throw]=Thread => IndexThrow
Threads[9]=throw => RightHandSideThrow
Threads[9]=Thread => ArrayIndexOutOfBoundsException
which indicates that the attempt to store a reference to a Threads[1]=StringBuffer => ArrayStoreException
StringBuffer into an array whose components are of type Thread throws an ArrayStoreException. The code is type-correct at compile time: the assignment has a left-hand side of type Object[] and a right-hand side of type Object. At run time, the first actual argument to method testFour is a reference to an instance of "array of Thread" and the third actual argument is a reference to an instance of class StringBuffer.15.26.2 Compound Assignment Operators
A compound assignment expression of the form E1 op= E2 is equivalent to E1 = (T)((E1) op (E2)), where T is the type of E1, except that E1 is evaluated only once.
and results in
short x = 3;
x += 4.6;
x having the value 7 because it is equivalent to:
At run time, the expression is evaluated in one of two ways. If the left-hand operand expression is not an array access expression, then four steps are required:
short x = 3;
x = (short)(x + 4.6);
If the left-hand operand expression is an array access expression (§15.13), then many steps are required:
Otherwise, the null, then no assignment occurs and a NullPointerException is thrown.
ArrayIndexOutOfBoundsException is thrown.
String. Because class String is a final class, S must also be String. Therefore the run-time check that is sometimes required for the simple assignment operator is never required for a compound assignment operator.
+=). If this operation completes abruptly, then the assignment expression completes abruptly for the same reason and no assignment occurs.
String result of the binary operation is stored into the array component.
This program prints:class ArrayReferenceThrow extends RuntimeException { }
class IndexThrow extends RuntimeException { }
class RightHandSideThrow extends RuntimeException { }
class IllustrateCompoundArrayAssignment {
static String[] strings = { "Simon", "Garfunkel" };
static double[] doubles = { Math.E, Math.PI };
static String[] stringsThrow() {
throw new ArrayReferenceThrow();
}
static double[] doublesThrow() {
throw new ArrayReferenceThrow();
}
static int indexThrow() { throw new IndexThrow(); }
static String stringThrow() {
throw new RightHandSideThrow();
}
static double doubleThrow() {
throw new RightHandSideThrow();
}
static String name(Object q) {
String sq = q.getClass().getName();
int k = sq.lastIndexOf('.');
return (k < 0) ? sq : sq.substring(k+1);
}
static void testEight(String[] x, double[] z, int j) {
String sx = (x == null) ? "null" : "Strings";
String sz = (z == null) ? "null" : "doubles";
System.out.println();
try {
System.out.print(sx + "[throw]+=throw => ");
x[indexThrow()] += stringThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print(sz + "[throw]+=throw => ");
z[indexThrow()] += doubleThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print(sx + "[throw]+=\"heh\" => ");
x[indexThrow()] += "heh";
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print(sz + "[throw]+=12345 => ");
z[indexThrow()] += 12345;
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print(sx + "[" + j + "]+=throw => ");
x[j] += stringThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print(sz + "[" + j + "]+=throw => ");
z[j] += doubleThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print(sx + "[" + j + "]+=\"heh\" => ");
x[j] += "heh";
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print(sz + "[" + j + "]+=12345 => ");
z[j] += 12345;
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
}
public static void main(String[] args) {
try {
System.out.print("throw[throw]+=throw => ");
stringsThrow()[indexThrow()] += stringThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print("throw[throw]+=throw => ");
doublesThrow()[indexThrow()] += doubleThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print("throw[throw]+=\"heh\" => ");
stringsThrow()[indexThrow()] += "heh";
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print("throw[throw]+=12345 => ");
doublesThrow()[indexThrow()] += 12345;
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print("throw[1]+=throw => ");
stringsThrow()[1] += stringThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print("throw[1]+=throw => ");
doublesThrow()[1] += doubleThrow();
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print("throw[1]+=\"heh\" => ");
stringsThrow()[1] += "heh";
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
try {
System.out.print("throw[1]+=12345 => ");
doublesThrow()[1] += 12345;
System.out.println("Okay!");
} catch (Throwable e) { System.out.println(name(e)); }
testEight(null, null, 1);
testEight(null, null, 9);
testEight(strings, doubles, 1);
testEight(strings, doubles, 9);
}
}
The most interesting cases of the lot are tenth and eleventh from the end:throw[throw]+=throw => ArrayReferenceThrow
throw[throw]+=throw => ArrayReferenceThrow
throw[throw]+="heh" => ArrayReferenceThrow
throw[throw]+=12345 => ArrayReferenceThrow
throw[1]+=throw => ArrayReferenceThrow
throw[1]+=throw => ArrayReferenceThrow
throw[1]+="heh" => ArrayReferenceThrow
throw[1]+=12345 => ArrayReferenceThrow
null[throw]+=throw => IndexThrow
null[throw]+=throw => IndexThrow
null[throw]+="heh" => IndexThrow
null[throw]+=12345 => IndexThrow
null[1]+=throw => NullPointerException
null[1]+=throw => NullPointerException
null[1]+="heh" => NullPointerException
null[1]+=12345 => NullPointerException
null[throw]+=throw => IndexThrow
null[throw]+=throw => IndexThrow
null[throw]+="heh" => IndexThrow
null[throw]+=12345 => IndexThrow
null[9]+=throw => NullPointerException
null[9]+=throw => NullPointerException
null[9]+="heh" => NullPointerException
null[9]+=12345 => NullPointerException
Strings[throw]+=throw => IndexThrow
doubles[throw]+=throw => IndexThrow
Strings[throw]+="heh" => IndexThrow
doubles[throw]+=12345 => IndexThrow
Strings[1]+=throw => RightHandSideThrow
doubles[1]+=throw => RightHandSideThrow
Strings[1]+="heh" => Okay!
doubles[1]+=12345 => Okay!
Strings[throw]+=throw => IndexThrow
doubles[throw]+=throw => IndexThrow
Strings[throw]+="heh" => IndexThrow
doubles[throw]+=12345 => IndexThrow
Strings[9]+=throw => ArrayIndexOutOfBoundsException
doubles[9]+=throw => ArrayIndexOutOfBoundsException
Strings[9]+="heh" => ArrayIndexOutOfBoundsException
doubles[9]+=12345 => ArrayIndexOutOfBoundsException
They are the cases where a right-hand side that throws an exception actually gets to throw the exception; moreover, they are the only such cases in the lot. This demonstrates that the evaluation of the right-hand operand indeed occurs after the checks for a null array reference value and an out-of-bounds index value.Strings[1]+=throw => RightHandSideThrow
doubles[1]+=throw => RightHandSideThrow
This program prints:class Test {
public static void main(String[] args) {
int k = 1;
int[] a = { 1 };
k += (k = 4) * (k + 2);
a[0] += (a[0] = 4) * (a[0] + 2);
System.out.println("k==" + k + " and a[0]==" + a[0]);
}
}
The value k==25 and a[0]==25
1 of k is saved by the compound assignment operator += before its right-hand operand (k = 4) * (k + 2) is evaluated. Evaluation of this right-hand operand then assigns 4 to k, calculates the value 6 for k + 2, and then multiplies 4 by 6 to get 24. This is added to the saved value 1 to get 25, which is then stored into k by the += operator. An identical analysis applies to the case that uses a[0]. In short, the statements
behave in exactly the same manner as the statements:k += (k = 4) * (k + 2);
a[0] += (a[0] = 4) * (a[0] + 2);
k = k + (k = 4) * (k + 2);
a[0] = a[0] + (a[0] = 4) * (a[0] + 2);
15.27 Expression
An Expression is any assignment expression:
Expression:
AssignmentExpression
15.28 Constant Expression
ConstantExpression:
Expression
String that does not complete abruptly and is composed using only the following:
Compile-time constant expressions are used in String (§3.10.5)
String
+, -, ~, and ! (but not ++ or --)
*, /, and %
+ and -
<<, >>, and >>>
<, <=, >, and >= (but not instanceof)
== and !=
&, ^, and |
&& and the conditional-or operator ||
? :
. Identifier that refer to constant variables (§4.12.4).
case labels in switch statements (§14.11) and have a special significance for assignment conversion (§5.2). Compile-time constants of type String are always "interned" so as to share unique instances, using the method String.intern.true
(short)(1*2*3*4*5*6)
Integer.MAX_VALUE / 2
2.0 * Math.PI
"The integer " + Long.MAX_VALUE + " is mighty big."
Contents | Prev | Next | Index
Java Language Specification
Third Edition
Please send any comments or corrections via our